00:01.30
この画面が切り替わらない時は
下をクリックしてください





この画面が切り替わらない時は
下をクリックしてください





ルール
使い方
もっと教えて
次の一手
[R?C?]のRは行・Y軸(row)/Cは列・X軸(colmn)です
ナンプレのルール
1つの行に同じ数字が入ってはいけません
| 1 | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
1つの列に同じ数字が入ってはいけません
| 1 |
| 1 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
3×3のBOXに同じ数字が入ってはいけません
| 1 | 1 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
[上部]モード
[最初から]ナンプレを全てクリアします
[全候補クリア]候補数字を全てクリアします[候補]ボタンと合わせてお使いください
[入力]モード
[C]マスをクリアします
[↩]1つ前に戻ります50回までです。
[中断]現在の状態を保存し戻ります
[ヒント①]次に使うテクニックを教えてくれます。間違っているコマを赤で表示。
[ヒント②]次にヒントを教えてくれます。間違っているコマを赤で表示。
[次の1手]現在解答中の状況から1手先を見ることができます。30秒プラスされます。
[候補]空白のセルに候補を自動で入力します。
[数字大]選択セルに数字を入力します。ダブルクリックでも入力できます。同じ数字の場合クリアします
[数字小]選択セルに候補数字を入力します。ダブルクリックでも入力できます。同じ候補数字の場合クリアします
[メモ]モード
[全消]ペンやスタンプを全て消します
[消しゴム]ペンやスタンプを消します
[🖋]ペンツールです。自由に描くことができます
[◯][×][△]スタンプです
[■]色を選択します。
[数字大]クリックすると数字に色がつきます。2回目は消えます
[数字小]クリックすると候補数字に色がつきます。2回目は消えます
単一候補(シングルカンディデート)
例:下の[9]ようにセルに1つしか候補が無い場合数字が確定します
| 23 6 7 | 3 7 9 | 2 9 | 1 | 3 4 6 8 | 5 | 23 89 | 9 | 2 89 |
ヒドゥンシングル
例:下のピンクのセルは[289]と候補が3つありますが、行に[2]が1つしか無い場合は数字が[2]で確定します。行だけでなく列・ボックスもチェックしてください。
| 1 6 | 1 4 | 6 9 | 5 | 3 4 6 | 3 6 | 6 8 | 7 | 2 89 |
ネイキッドペア
例:下のピンクのセルは[46][46]と同じ候補が2つが2つのセルに入っています。この場合[4][6]か[6][4]になるので、同じ行の[4]と[6]を削除することができます。行だけでなく列・ボックスもチェックしてください。(3つの候補が3つのセル、4つの候補が4つのセルでも同様です。)
| 8 | 2 6 | 6 9 | 4 6 | 4 6 | 5 | 1 | 2 7 | 3 7 9 |
ヒドゥンペア
例:[58]は下のピンクの2つのセルにしか出ません。この場合[5][8]か[8][5]になります。セル内の[58]以外を削除することができます。行だけでなく列・ボックスもチェックしてください。(3つの候補が3つのセル、4つの候補が4つのセルでも同様です。)
| 1 45 789 | 1 4 7 | 3 | 2 | 1 4 6 9 | 4 6 9 | 1 4 6 9 | 1 4 7 9 | 1 56 789 |
↓
| 5 8 | 1 4 7 | 3 | 2 | 1 4 6 9 | 4 6 9 | 1 4 6 9 | 1 4 7 9 | 5 8 |
ネイキッドクアッド
例:9つめのBOXの中に[2459]はピンクの4つのセルにしか出ません。ネイキッドペアなどと同様にこの場合[2][4][5][9]のいずれかがこの4つのセルに入りますので。BOX内のほかのセルから[2459]を削除できます。BOXだけでなく行・列もチェックしてください。(3つの候補が3つのセル、4つの候補が4つのセルでも同様です。)
| 8 | 4 | 1 | 3 | 2 | 7 | 56 | 56 | 9 |
| 2 9 | 5 9 | 2 5 | 8 | 4 | 6 | 1 | 3 | 7 |
| 6 | 3 | 7 | 5 | 9 | 1 | 4 8 | 2 4 | 2 8 |
| 5 | 8 | 9 | 1 | 3 | 2 | 6 7 | 6 7 | 4 |
| 3 | 7 | 6 | 4 | 8 | 9 | 2 | 1 5 | 1 5 |
| 1 | 2 | 4 | 7 | 6 | 5 | 9 | 8 | 3 |
| 2 4 9 | 6 | 2 8 | 2 9 | 5 | 3 4 | 3 4 78 | 12 4 7 9 | 12 8 |
| 2 4 9 | 1 | 2 5 8 | 2 9 | 7 | 3 4 | 3 45 8 | 2 45 9 | 6 |
| 7 | 5 9 | 3 | 6 | 1 | 8 | 45 | 2 45 9 | 2 5 |
ヒドゥンクアッド
例:[1257]は下のピンクの4つのセルにしか出ません。ということは4つのセルは[1257]で確定しますので、[1257]以外を削除することができます。行だけでなく列・ボックスもチェックしてください。
| 3 4 6 89 | 3 6 89 | 3 4 6 8 | 12 9 | 2 5 7 | 3 4 | 4 6 8 | 1 4 6 7 | 5 78 |
↓
| 3 4 6 89 | 3 6 89 | 3 4 6 8 | 12 9 | 2 5 7 | 3 4 | 4 6 8 | 1 4 6 7 | 5 78 |
ポインティングペア
例:中央のボックスには[8]が2つしかないためどちらかに[8]が入ります。そのため延長線上の[8]を消すことができます。
| 1 | 3 4 6 | 3 4 6 8 | 7 | 23 4 | 23 | 6 8 | 9 | 5 |
| 3 56 8 | 2 | 3 456 8 | 9 | 3 4 | 56 | 1 | 6 8 | 7 |
| 56 8 | 9 | 7 | 1 5 8 | 1 5 8 | 1 56 | 2 | 3 | 4 |
ボックスライン
例:2行目に[6]は中央のBOXにしかないため、BOX内の他の[6]は削除できます。
| 4 | 2 6 7 | 1 | 2 6 7 9 | 2 6 7 9 | 3 | 8 | 5 | 2 6 7 |
| 5 | 9 | 3 | 4 6 7 | 8 | 4 6 7 | 1 | 4 7 | 2 |
| 78 | 6 78 | 2 | 5 | 4 6 7 | 1 | 9 | 3 | 4 6 7 |
X-ウィング
例:2列目と7列目は[3]が2つづつしかない。行も同じなのでX-ウィング成立。(ピンクのセル)4つのセルのどこかに[3]が入ります。そのため行方向の延長線上の[3]を消すことができます。
候補数字が2回しかでてこない行か列のペアを探しましょう
| 3 8 | 9 | 3 4 8 | 1 3 4 | 6 | 7 | 5 | 2 | 1 3 4 |
| 5 | 1 | 6 | 3 4 | 8 | 2 | 9 | 3 4 | 7 |
| 7 | 2 | 3 4 | 5 | 1 3 4 | 9 | 6 | 1 3 4 | 8 |
| 3 4 | 5 | 2 | 7 | 9 | 8 | 1 | 6 | 3 4 |
| 89 | 3 6 | 89 | 2 | 1 3 4 |
1 3 4 6 | 3 4 | 7 | 5 |
| 3 4 6 | 7 | 1 | 3 4 6 | 5 | 3 4 6 | 2 | 8 | 9 |
| 1 6 9 | 3 6 | 7 | 8 | 1 3 4 |
1 3 45 | 3 4 |
1 3 45 9 | 2 |
| 1 3 9 | 8 | 3 9 | 1 3 4 9 | 2 | 1 3 45 | 7 | 1 3 45 9 | 6 |
| 2 | 4 | 5 | 1 3 6 9 | 7 | 1 3 6 | 8 | 1 3 9 | 1 3 |
Y-ウィング
例:[67]を中心にBOX内に[56]のセル、行内に[57]のセルでY-ウィング成立。(ピンクのセル)[67]が[6]でも[7]でも[56]か[57]に[5]が決定しますので、両方のクロスするセルから[5]を削除できます。
[BOX内,行内][BOX内,列内][列内,行内]のパターンで成立します。
| 8 | 5 7 | 3 | 1 | 9 | 4 6 | 2 4 | 56 | 2 6 7 |
| 9 | 5 7 | 2 | 3 5 | 8 | 4 6 | 3 4 | 1 | 6 7 |
XYZ-ウィング
例:1つのセルに候補が3つ[XYZ]、同じBOX内にそれの候補のうち2つ[XZ]、同じようにそれとは重ならないBOX外の延長線上に候補が2つ[YZ]で条件成立。3つのセルのいずれかに[Z]が入るので、ベースとなるセルのBOXと延長線上のセルとの共通部分には[Z]は入れません。
| Z | XYZ | Z | YZ | |||||
| XZ | ||||||||
具体的には下図のようになります
| 7 | 4 89 | 3 4 8 | 1 | 3 8 | 6 | 5 | 89 | 2 |
| 1 8 | 2 | 1 3 6 8 | 3 4 89 | 5 | 3 4 89 | 7 | 1 89 | 1 6 89 |
| 5 | 1 89 | 1 6 8 | 2 89 | 7 | 2 89 | 4 | 3 | 1 6 89 |
下のような[XY][XZ][YZ]の場合はY-ウイングです
| Z | XY | Z | YZ | |||||
| XZ | Z | X | Z | |||||
シングルチェーン
例:[5]の数字のペアを行列ボックスで探します。ペアなので片方に[5]が入ると片方には[5]は入りません。そうなるとさらに[5]が入るセルが出てきます。シングルチェーンはこのように1つの数字に注目して繋いでいき、スタートセルの[5]を入れる入れない2パターンを比べ共通して削除できるセルやから候補を削除します。
もし片方のチェーンに矛盾が生じた場合はそのチェーンは全て間違いということになります。
下の例では青のチェーンと緑のチェーンの可能性があり、どちらになっても赤い文字の[5]は削除できます。
メモ機能を使おう:チェーン系はメモ機能で候補数字に色つけすると便利です。
| 1 45 | 1 5 | 7 | 2 5 | 8 | 3 | 6 | 1 4 9 | 12 4 9 |
| 1 45 | 3 | 9 | 7 | 2 5 | 6 | 8 | 1 4 | 12 4 |
| 8 | 2 | 6 | 4 | 1 | 9 | 7 | 5 | 3 |
| 6 | 4 | 2 5 | 1 | 9 | 2 5 | 3 | 8 | 7 |
| 1 5 9 | 8 | 12 5 | 3 | 6 | 7 | 2 45 | 1 4 9 | 1 45 9 |
| 1 9 | 7 | 3 | 2 5 | 4 | 8 | 2 5 | 6 | 1 9 |
| 3 | 9 | 1 5 | 8 | 7 | 1 4 | 45 | 2 | 6 |
| 7 | 6 | 4 | 9 | 2 5 | 2 5 | 1 | 3 | 8 |
| 2 | 1 5 | 8 | 6 | 3 | 1 4 | 9 | 7 | 45 |
ソードフィッシュ
例:X-ウィングの9つ版です。下の例では[8]が行方向に3つしかない行が2つ、行方向に2つしかない行が1つあり、それぞれの列は同じです。(ピンクのセル)このような場合ピンクのセルのいずれかに[8]が入りますので、列方向の[8]を削除することができます。
(これは左下が欠落しているのですが、左下を入れると9つのセルとなります)
| 1 89 | 5 | 89 | 4 7 | 3 8 | 1 7 | 6 | 4 9 | 2 |
| 6 | 4 | 2 | 8 | 9 | 5 | 3 | 1 | 7 |
| 1 9 | 3 | 7 | 4 6 | 2 | 1 6 | 8 | 45 9 | 5 9 |
| 89 | 2 | 3 8 | 5 | 1 8 | 4 | 7 | 6 9 | 1 6 9 |
| 4 | 89 | 6 | 3 7 | 1 78 | 3 78 | 5 | 2 | 1 9 |
| 5 | 7 | 1 | 9 | 6 | 2 | 4 | 8 | 3 |
| 2 | 1 | 4 | 3 6 7 | 5 78 | 3 6 78 | 9 | 56 | 56 8 |
| 7 | 6 | 5 8 | 1 | 5 8 | 9 | 2 | 3 | 4 |
| 3 | 89 | 5 89 | 2 | 4 | 6 8 | 1 | 7 | 56 8 |
XYZ-ウィング
例:1つのセルに候補が3つ[XYZ]、同じBOX内にそれの候補のうち2つ[XZ]、同じようにそれとは重ならないBOX外の延長線上に候補が2つ[YZ]で条件成立。3つのセルのいずれかに[Z]が入るので、ベースとなるセルのBOXと延長線上のセルとの共通部分には[Z]は入れません。
| Z | XYZ | Z | YZ | |||||
| XZ | ||||||||
具体的には下図のようになります
| 7 | 4 89 | 3 4 8 | 1 | 3 8 | 6 | 5 | 89 | 2 |
| 1 8 | 2 | 1 3 6 8 | 3 4 89 | 5 | 3 4 89 | 7 | 1 89 | 1 6 89 |
| 5 | 1 89 | 1 6 8 | 2 89 | 7 | 2 89 | 4 | 3 | 1 6 89 |
下のような[XY][XZ][YZ]の場合はY-ウイングです
| Z | XY | Z | YZ | |||||
| XZ | Z | X | Z | |||||
X-サイクル
1つの数字で強リンク・弱リンクで1周します。(図の下に説明)2つのリンクを作ると共通で削除できるセルができあがります。
例:下図ではX-サイクル(x-cycles):3が:[R2C1]=強=>[R2C6]=弱=>[R5C6]=強=>[R5C3]=強=>[R3C3]=弱=>[R2C1]で成立しています。
[R2C1]か[R5C3]のどちらかに必ず[3]が入ります。どちらに[3]が来ても[R3C3]と[R4C1]に3は入ることができません。
問題を解くときはメモ機能を活用しましょう。

強リンク:行にその数字が2つしかない場合片方がその数字だともう片方にはその数字がはいりません。
| 2 6 7 | 456 | 45 7 | 8 | 2 7 | 9 | 4 6 7 | 3 | 1 |
弱リンク:行にその数字が3つ以上あると、1つに入らないことがわかっても、その数字がどこに入るかはわかりません。
| 6 7 | 1 | 4 7 | 2 | 8 | 4 6 7 | 9 | 5 | 3 |
しかし1つにその数字が決まると残りにその数字は入りません。入らないセルに別の強リンクがあればそちらにその数字は入ることになります。
| 6 7 | 1 | 4 7 | 2 | 8 | 4 6 7 | 9 | 5 | 3 |
ルール2
最後は弱リンクでいいのですがもし強リンクでしかもチェーンの数が奇数の場合ルール2が成立します。
[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=強=>[1](OFFスタート)
最後のセル=最初のセルなので最初OFFでスタートしているにもかかわらず最後がONになってしまいます。
矛盾するので最初がOFFということにはならずに最初のセルは[ON]で確定します。
ルール3
最後は弱リンクでいいので、[弱]=>[弱]となる場合がでてきます。上と同様チェーンの数が奇数の場合で最後が[弱]=>[弱]の場合ルール3が成立します。
[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=弱=>[?](OFFスタート)
[1]=強=>[1]=弱=>[?]=強=>[?]=弱=>[?]=強=>[?]=弱=>[1]=弱=>[1](ONスタート)
最後のセル=最初のセルなのでONスタートの場合逆回りも考えます。最後のセルのとなりはOFFとなります。
OFFスタートでもONスタートでも[弱]=>[弱]で挟まれた最後のセルの1つまえは必ず[OFF]になります。
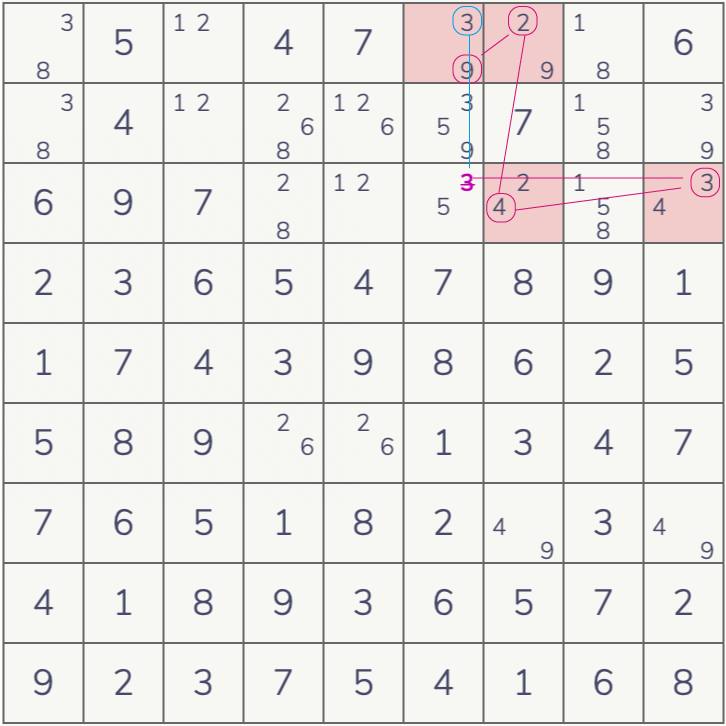
BUG
全てが2択候補で1つのセルだけ3択になっていて、行列BOXの同じ数字が2回づつ、その条件が成立すると3択数字のあまった1つの数字が確定します。
例:下図が具体例です。9だけが3行列BOXに3回づつでてきます。この場合[9]で確定します。
すべて2択だとナンプレの回答が2種類できてしまう。それだとナンプレとして成立しないので3択のあふれた1つを決定するというのが原理です。
| 9 | 6 | 5 | 7 | 2 | 8 | 1 4 | 3 4 | 1 3 |
| 7 | 8 | 4 | 3 | 1 | 5 | 6 9 | 2 6 | 2 9 |
| 2 | 3 | 1 | 4 | 9 | 6 | 5 8 | 78 | 5 7 |
| 1 | 5 | 8 | 9 | 3 | 2 | 4 6 | 6 7 | 4 7 |
| 4 | 9 | 3 | 1 | 6 | 7 | 5 8 | 2 8 | 2 5 |
| 6 | 7 | 2 | 8 | 5 | 4 | 1 9 | 3 9 | 1 3 |
| 3 8 | 12 | 6 9 | 2 6 | 4 8 | 1 3 9 | 7 | 5 | 4 9 |
| 3 5 | 4 | 6 9 | 56 | 7 | 3 9 | 2 | 1 | 8 |
| 5 8 | 12 | 7 | 2 5 | 4 8 | 1 9 | 3 | 4 9 | 6 |
XY-チェーン
候補が2つ入ったセルが4つ以上で、始まりと終わりが同じ数字になるチェーンを探します。例えば[12]=[23]=[34]=[41]のように[1]で始まり[1]で終わるチェーン。
その場合最初が[1]なら[1][?][?][?]。最初が[2]なら[2][3][4][1]になります。
最初のセルと最後のセルのどちらかに[1]が入るので共通の削除候補は消せます。
例:下図が具体例です。XY-チェーン(xy-chain):3が:[R1C6][R1C7][R3C7][R3C9]で成立しています。最初と最後どちらに[3]が来ても[R3C6]に[3]は入ることができません。
3Dメデューサ
片方に入ったらもう片方には入らない強リンクで全て繋いでいきます。数字はなんでもいいです。
そうするとメデューサ髪の毛のようにチェーンがからまりあった状態になります。ここでON/OFFの2つのチェーンを色つけします。
ルール1片方のチェーンが1つのセルに2つの候補が正解になってしまう(例:ONの場合[1,8]が同セルに入る):矛盾したらその色は全部削除です。
ルール2片方のチェーンが行列BOXで候補が重なってしまう(例:OFFの場合8が同じ行2つできる):矛盾したらその色は全部削除です。
ルール32つのチェーンのどちらでも1つのセルに候補が入る(例:セルA[1,6,8]にON[1]OFF[8]だと[6]は削除):その候補以外は削除できます
ルール42つのチェーンのどちらでも共通で削除できる候補(例:ONの場合[R1C1]に[1]、OFFの場合[R1C9]に[1]なら他の[R1]の[1]は全て削除):その候補は削除できます
ルール52つのチェーンのどちらでも共通で削除できる候補(例:ONの場合セルA[1,6]に[1]、OFFの場合その隣のセルが[6]ならセルAに[6]は入れない):その候補は削除できます
ルール6片方のチェーンの場合空白になるセルができてしまう(例:ONの場合セルAに[1]、セルBに[5]、セルABの延長に[2,5]のセルがあるとONの場合[2,5]はなくなってしまう):矛盾したらその色は全部削除です。
例:下図がルール2の具体例です。[R1C8]に[8]を入れない場合、行7に8が複数確定します。矛盾するので[R1C8]は[8]になります。
ゼリーフィッシュ
X-ウィング・ソードフィッシュの4つ版です。行に4つしか数字がない状態で、列が同じだとどこかにその数字が入るので同じ列の他の行からその数字を削除できます。
例:下図が具体例です。[6]が4つ以内の行が4つ。どれも同じ列です。(欠落あり)こういう場合はどこかに[6]が入るので、同じ列の[6]を削除することができます。
| 3 56 | 1 3 456 | 1 3 4 6 | 456 7 9 | 3 45 7 9 | 4 6 | 2 8 | 56 7 | 2 8 |
| 7 | 3 56 | 2 | 1 | 3 56 | 8 | 4 | 9 | 56 |
| 9 | 456 | 8 | 456 7 | 456 7 | 2 | 1 5 | 3 | 1 56 7 |
| 23 6 8 | 23 6 78 | 3 6 7 | 4 6 7 9 | 12 4 6 7 9 | 1 4 6 | 1 5 89 | 56 | 1 3 56 8 |
| 1 | 2 6 78 | 5 | 6 7 9 | 2 6 7 9 | 3 | 89 | 4 | 6 8 |
| 4 | 3 6 | 9 | 8 | 1 6 | 5 | 7 | 2 | 1 3 6 |
| 56 8 | 45 8 | 4 6 | 2 | 456 8 | 7 | 3 | 1 | 9 |
| 23 56 8 | 9 | 1 3 4 7 | 456 | 1 456 8 | 1 4 6 | 2 5 | 5 7 | 2 45 7 |
| 2 5 | 12 45 7 | 1 4 7 | 3 | 1 45 | 9 | 6 | 8 | 2 45 7 |
ユニークレクタングル
同じ行が2ペア・同じBOX内でペアがまず条件。例えば
[12][12]
[12][12]になると入れ替わり可能な重解になってしまいます。重解はナンプレの問題として成り立たないので他の選択肢が答えとなります。
タイプ 1
[12][12]
[12][123]なら必ず[3]になる。
タイプ 2
[12][12]
[123][123]ならどちらに[3]がきても共通に削除できるセルから削除。
タイプ 3
[12][12]
[123][124]で離れたところに[34]->それ以外のセルから[34]を消せる
タイプ 3b
[12][12]
[123][1234]で離れたところに[34][?4]->と[3][4]が3回づつでる。->[123][1234]は同じBOXが条件であまった1つのセルから[34]を消すことが可能
タイプ 4
[12][12]
[123][1234]←もしこの行でほかに[1]が入っているセルがなければ絶対にどちらかに[1]が来る。そのためもう片方に[2]はあり得ないため削除
例:下図が具体例です。[R2C7][R4C7][R2C9][R4C9]の全てのセルが[1,2]になると重解になってしまいます。
そのため[R4C9]には[1,2]は入れないません
| 2 7 | 1 | 2 7 | 3 | 6 | 5 | 9 | 4 | 8 |
| 5 | 3 | 4 | 8 | 9 | 7 | 12 | 6 | 12 |
| 9 | 8 | 6 | 2 | 4 | 1 | 7 | 3 5 | 3 5 |
| 12 4 6 8 | 4 6 9 | 12 8 | 7 | 5 | 3 | 12 | 1 9 | 12 4 6 9 |
| 12 4 6 7 | 4 6 7 | 3 | 1 4 | 8 | 9 | 5 | 1 7 | 12 4 6 7 |
| 1 4 7 | 45 7 9 | 1 5 7 | 1 4 | 2 | 6 | 3 | 8 | 1 4 7 9 |
| 3 | 2 | 1 5 | 6 | 7 | 4 | 8 | 1 5 9 | 1 5 9 |
| 1 6 7 | 6 7 | 9 | 5 | 3 | 8 | 4 | 2 | 1 7 |
| 4 78 | 45 7 | 5 78 | 9 | 1 | 2 | 6 | 3 5 7 | 3 5 7 |
SKループ
下図のように1行目・9行目・1列目・9列目を見ていきます。
左上のBOXでは横に1行目の候補 [7,8]が右上のBOXの1行目[7,8]と共通します。また縦は1列目の候補[2,7]が左下のBOXの1列目[2,7]と共通します。そして縦横のあまりが[3,5]で共通します。
この関係が右上、右下、左下でも同じようになりループしています。
時計回りに候補の数を計算します:
左上BOXのあまりの候補数:2 / 左上BOXの行の候補数:2
右上BOXのあまりの候補数:2 / 右上BOXの列の候補数:2
右下BOXのあまりの候補数:2 / 右下BOXの行の候補数:2
左下BOXのあまりの候補数:2 / 左下BOXの列の候補数:2
[2-2-2-2-2-2-2-2]となり16です。また空白セルも16なので数字がロックされ、行列のBOX外のセルからはそれぞれの共通候補、BOX内の行列以外のセルからはあまりの候補が削除できます。
この理屈は候補数が1の場合とかあまりが3の場合でも空白セルが16で候補の合計が16であれば成立しますし、空白セルが15の場合でも候補の数が15なら成立します。
| 4 | 3 5 78 | 3 78 | 6 | 1 3 89 | 1 5 7 | 789 | 1 789 | 2 |
| 2 5 7 | 56 78 | 9 | 5 78 | 1 4 8 | 12 45 7 | 3 | 1 4 6 78 | 1 6 7 |
| 23 7 | 1 | 23 6 78 | 3 789 | 3 4 89 | 2 4 7 | 4 6 789 | 5 | 6 7 9 |
| 7 9 | 2 | 6 7 | 1 | 5 | 3 | 6 789 | 6 789 | 4 |
| 1 3 5 7 9 | 3 5 7 | 1 3 7 | 4 | 6 | 8 | 2 5 7 9 | 12 7 9 | 1 3 5 7 9 |
| 8 | 3 456 | 1 3 4 6 | 2 | 7 | 9 | 56 | 1 6 | 1 3 56 |
| 23 7 | 3 4 78 | 5 | 3 789 | 3 4 89 | 4 6 7 | 1 | 2 4 6 7 9 | 6 7 9 |
| 12 7 | 9 | 12 4 78 | 5 78 | 1 4 8 | 1 456 7 | 2 456 7 | 3 | 56 7 |
| 6 | 3 4 7 | 1 3 4 7 | 3 5 7 9 | 2 | 1 45 7 | 45 7 9 | 4 7 9 | 8 |
グレーベースの候補がBOX内で共通しています。
※どうしてそうなるか
ヨコのペアが2行で縦のペアが2列で合計8つの数字。あふれ数字のペアは4つのBOXで8つの数字。
16個のセルに対して16の数字なので二国同盟と同様数字が確定するため他にその数字は入ることができません。
拡張ユニークレクタングル
ユニークレクタングルの3つ版です。同じ行での[123][123]のようなトリプルのペアが3つ分。
それぞれのペアが同じBOXで成立します。列方向の場所も共通していないといけません。
[123]は[13]のように欠落しててもかまいません。1つのセルだけ[1234]ならそのセルの答えは[4]になります。
そうでないとすべて[123]となり入れ替え可能となってしまいます。入れ替え可能だと重解になるのでナンプレの問題にはなりません。
下記が具体例です。[127]の行方向のペアが3行分あり、それぞれ同じBOXにいます。この場合あふれた[5]が解答になります。
| 6 | 4 | 8 | 3 | 9 | 5 | 1 7 | 12 7 | 12 7 |
| 2 | 5 | 3 | 8 | 7 | 1 | 6 | 4 | 9 |
| 1 9 | 1 9 | 7 | 2 | 6 | 4 | 8 | 3 | 5 |
| 5 | 6 | 4 | 7 9 | 1 3 | 8 | 1 3 9 | 12 7 | 12 |
| 1 9 | 3 7 | 12 9 | 4 | 1 3 | 2 6 9 | 1 3 5 7 9 | 1 56 7 | 8 |
| 8 | 3 7 | 12 9 | 6 7 9 | 5 | 2 6 9 | 1 3 7 9 | 1 6 7 | 4 |
| 3 | 8 | 1 9 | 56 9 | 4 | 6 9 | 2 | 1 5 7 | 1 7 |
| 7 | 2 | 5 | 1 | 8 | 3 | 4 | 9 | 6 |
| 4 | 1 9 | 6 | 5 9 | 2 | 7 | 1 5 | 8 | 3 |
ヒドゥンユニークレクタングル
下図はヒドゥンユニークレクタングルです。上の行が[16][16]のペアですが下は[136][1369]と候補が多くなっています。ユニークレクタングルのType3bに似ていますがちょっと違う考え方をします。
左上の[16]を中心に考えます。もし左上が[1]なら、その隣に[1]は入れないので[6]となります。
下の左側は[1]は入れないので[36]が候補となりますが、実は[6]が強リンクで、ここに[3]を入れると[6]が入る場所がなくなります。よって下の左側は[6]です。
ということは下の右側は[139]が残りますが、もし[1]が答えだと上の行[1][6]・下の行[6][1]でも上の行[6][1]・下の行[1][6]でもどっちも答えとなってしまい、ナンプレの問題として成り立ちません。
ということで左上が[1]の場合右下に[1]だけは入ることができません。
では左上が[6]ならどうでしょう。この場合はその隣が[1]となりやはり右下に[1]は入ることができません。
ということでいずれの場合も右下に[1]は入れないので候補[1]は削除できます。
このようにBOX内だけでなく上下の強リンクを考慮に入れて候補を削除するテクニックをヒドゥンユニークレクタングルといいます。
| 7 | 2 | 1 | 3 4 | 3 4 9 | 45 9 | 6 | 45 | 8 |
| 45 9 | 45 8 | 5 89 | 1 6 | 1 6 | 7 | 23 5 | 23 5 | 23 5 9 |
| 3 | 6 | 5 9 | 8 | 2 | 45 | 1 | 45 7 | 45 7 9 |
| 56 | 9 | 7 | 2 | 4 6 | 1 | 8 | 3 45 | 3 45 |
| 8 | 1 | 4 | 9 | 5 | 3 | 2 7 | 2 7 | 6 |
| 2 | 3 5 | 3 56 | 7 | 8 | 4 6 | 9 | 1 | 45 |
| 1 5 | 3 5 7 | 2 | 1 3 6 | 1 3 6 9 | 6 9 | 4 | 8 | 3 5 7 |
| 4 6 | 4 78 | 3 6 8 | 5 | 3 4 | 2 | 3 7 | 9 | 1 |
| 1 45 9 | 3 45 | 3 5 9 | 1 3 4 | 7 | 8 | 23 5 | 6 | 23 5 |
WXYZ-ウィング
例:1つのセルに候補が3つ[WXYZ]、同じBOX内にそれの候補のうち2つ[WZ]、同じようにそれとは重ならないBOX外の延長線上に候補が2つのセルが2つ[XZ][YZ]で条件成立。4つのセルのいずれかに[Z]が入るので、ベースとなるセルのBOXと延長線上のセルとの共通部分には[Z]は入れません。
[WZ]に[Z]が来たら当然BOX内に[Z]は入りません。[W]が来た時に一列に[XYZ]のネイキッドトリプル(三国同盟)ができると考えるとわかりやすいかと思います。
[WZ]だけは2文字でのこりは[XYZ]の2-3文字なんでも良いです。
| Z | WX YZ | Z | XZ | YZ | ||||
| WZ | ||||||||
具体的には下図のようになります
ピンクのセル[4569]があり同じBOX内に[59]があります。横を見るとピンクのセルの延長線上に[49][69]があります。
この場合ばっちりWXYZウイングとなります。どこかのセルに必ず[9]が入りますのでBOX内の横のライン上の[9]を消すことができます。
しかし実際にはイレギュラーパターンも多く出てきます。
| 4 9 | 5 7 9 | 6 | 5 9 | 1 | 8 | 4 7 | 3 | 2 |
| 23 45 9 | 2 5 9 | 1 | 7 | 3 4 6 9 | 456 9 | 4 9 | 6 9 | 8 |
| 3 4 9 | 3 7 9 | 8 | 3 6 9 | 3 4 6 9 | 2 | 1 | 4 6 7 9 | 5 |
コアとなるセルに[Z]が無いパターン:この場合飛び出しセルかBOX外のどちらかに[Z]が入るので飛び出しセルとの共通部分の[Z]を削除できます。
| Z | WX Y | Z | XZ | YZ | ||||
| WZ | Z | Z | Z | |||||
同じBOX内のセルが[WXY]が2つある([Z]が無いパターン):この場合も飛び出しセルかBOX外のどちらかに[Z]が入るので飛び出しセルとの共通部分の[Z]を削除できます。
| WX Y | WX Y | Z | YZ | |||||
| WZ | Z | Z | Z | |||||
コアとなるセルに[Z]が無いパターン2:この場合も飛び出しセルかBOX外のどちらかに[Z]が入るので飛び出しセルとの共通部分の[Z]を削除できます。
飛び出しセルに[W]が来た場合コアセルが[X]になり残り2つが[YZ]のネイキッドペアになります
| Z | WX | Z | XYZ | XYZ | ||||
| WZ | Z | Z | Z | |||||
アラインペアエクスクルージョン
任意の2つのセルを引っ張り出し、その2つのセルのすべての組み合わせを試します。
例えば[24]のセルと[258]のセルがあったら組み合わせは[2-2][2-5][2-8][4-2][4-5][4-8]です。
もし[2-8]のパターンで強リンクを見ていくと矛盾し、[4-8]のパターンでも強リンクを見ていくと矛盾するなら[258]のセルに[8]は入らないということになり[8]を削ることができます。
仮置きっぽいですが、同じBOXとか同じ行の任意の2つのセルにヤマを張って候補が2択などのセルを探していくのがポイントです。
例:下図が具体例です。[57][3567]ですが[5-5]はあり得ないので[7-5]を見てみます。ところが右のセルが[5]だと黄色いセルに入る候補がなくなってしまいます。(さらに下図)
ということで右側のセルに[5]を入れることはできません。
| 4 | 5 7 | 3 5 | 1 | 8 | 3 6 | 9 | 3 56 7 | 2 |
| 1 | 23 5 7 | 6 | 2 4 7 | 23 7 | 9 | 3 5 7 | 8 | 45 |
| 8 | 23 7 9 | 3 9 | 2 4 7 | 23 6 | 5 | 1 | 3 6 7 | 4 7 |
| 5 | 6 | 1 | 9 | 3 7 | 2 | 3 4 7 | 3 4 7 | 8 |
| 3 | 8 | 2 | 5 7 | 1 | 4 | 6 | 9 | 5 7 |
| 9 | 4 | 7 | 8 | 3 56 | 3 6 | 3 5 | 2 | 1 |
| 6 | 3 5 | 8 | 23 5 | 4 | 1 | 2 5 7 | 5 7 | 9 |
| 2 | 1 | 3 45 9 | 3 5 | 5 9 | 7 | 8 | 45 | 6 |
| 7 | 5 9 | 45 9 | 6 | 2 5 9 | 8 | 2 45 | 1 | 3 |
左のセルと[7]、右のセルを[5]にすると
| 4 | 7 | 3 5 | 1 | 8 | 3 6 | 9 | 5 | 2 |
| 1 | 23 5 7 | 6 | 2 4 7 | 23 7 | 9 | 3 5 7 | 8 | 45 |
| 8 | 23 7 9 | 3 9 | 2 4 7 | 23 6 | 5 | 1 | 3 6 7 | 4 7 |
| 5 | 6 | 1 | 9 | 3 7 | 2 | 3 4 7 | 3 4 7 | 8 |
| 3 | 8 | 2 | 5 7 | 1 | 4 | 6 | 9 | 5 7 |
| 9 | 4 | 7 | 8 | 3 56 | 3 6 | 3 5 | 2 | 1 |
| 6 | 3 5 | 8 | 23 5 | 4 | 1 | 2 5 7 | 5 7 | 9 |
| 2 | 1 | 3 45 9 | 3 5 | 5 9 | 7 | 8 | 45 | 6 |
| 7 | 5 9 | 45 9 | 6 | 2 5 9 | 8 | 2 45 | 1 | 3 |
エグゾセ
1つのBOX内の横並びで候補が3つ以上のペアを探します。[123][12]や[1234][14]などこれがベースペアとなります。
(ベースペアと同じBOXで隣のセルはベースペア候補を含んでいてはいけません。例題調べたところ確定数字が入っている状態でした)
隣のBOXのベースペアとは違う行にベースペア候補を全て含むセルを探します。これがターゲットセル1(T1)です。
さらに隣のBOXのベースペアともターゲットセル1とも違う行に同じようにベースペア候補を全て含むセルを探します。これがターゲットセル2(T2)です。
ターゲットセルの列のもう一つのあまったセルはコンパニオンセル(C1C2)です。数字が入っている状態か候補でもベースペア候補を含んではいけません。
ベースペアではない列(クロスラインベース(CLB))とターゲットセル1・2の列(クロスライン)に「Sセル」ベースペア候補が入る組み合わせは2回以内でないといけません。(例えばベースペア[123]のうち[1]がSセルに3回入ることができる場合は成立していません)これで条件成立。ターゲットセル1・2のベースペア候補以外の数字を消すことができます。
行列は入れ替えて考えてOKです。
| B | B | * | * | * | ||||
| * | T1 | M2 | M2 | C2 | ||||
| * | C1 | T2 | M1 | M1 | ||||
| S | S | S | ||||||
| S | S | S | ||||||
| S | S | S | ||||||
| S | S | S | ||||||
| S | S | S | ||||||
| S | S | S | ||||||
| CLB | CL1 | CL2 |
例:下図が具体例です。ALS(ほぼロックされたセット)の一種のようです。ALSはこちらで解説しています。
例えば赤いセルの左側が[2]だとすると、同じBOXに[2]は入れません。ということは水色のCLBに[2]が入り、CL1かCL2には[2]が入らないセルが出てきます。ということはT1かT2は必ず[2]になります。
ベースセルに入った数字が必ずターゲットセルに来るためベースペアが[268]ならターゲットセルも[268]になります。
| 3 | 12 4 6 8 | 2 4 6 8 | 5 | 4 6 7 9 | 2 4 789 | 1 6 789 | 12 6 89 | 12 7 9 |
| 7 | 12 4 6 8 | 5 | 2 4 6 8 | 4 6 9 | 2 4 89 | 1 6 89 | 3 | 12 9 |
| 2 6 8 | 9 | 2 6 8 | 23 6 8 | 1 | 23 78 | 56 78 | 2 56 8 | 4 |
| 2 4 6 8 | 5 | 23 4 6 8 | 9 | 3 4 | 1 8 | 1 4 6 | 7 | 123 |
| 4 6 9 | 4 6 7 | 1 | 3 4 | 2 | 5 7 | 3 456 9 | 56 9 | 8 |
| 2 4 89 | 2 4 78 | 23 4 789 | 1 8 | 5 7 | 6 | 1 4 9 | 12 9 | 123 5 9 |
| 2 56 89 | 3 | 2 6 89 | 7 | 56 9 | 12 9 | 1 89 | 4 | 1 5 9 |
| 1 | 2 4 7 | 2 4 7 9 | 23 4 | 8 | 23 45 9 | 3 7 | 5 9 | 6 |
| 456 89 | 4 6 8 | 4 6 789 | 1 4 6 | 3 456 9 | 1 4 9 | 2 | 1 89 | 3 7 |
グループXサイクル
X-サイクルは1つの数字1つのセルでチェーンをつないで行くのですが、いくつかの数字をグループにして考えるバージョンです。
F 12 | F 12 5 | 4 | 9 | 3 | 8 | E 12 5 7 | 6 | 2 7 |
上の場合はXサイクルだと弱リンクとなりますが
左の2つを1つの数字と考えるとグループXサイクルでは強リンクになります。
C 12 45 7 9 |
C 12 5 7 |
2 4 7 |
D 1 4 7 9 |
3 | 6 |
| 2 45 7 9 |
2 5 7 |
8 |
上の場合は上段2つと中段1つが強リンクとして考えます。
また左列2つと中央の列1つも強リンクです。
グループにする数字があると候補が増える分X-サイクルよりもたくさんの可能性が広がります。
具体的にはX-サイクル同様 強リンク->弱リンク->強リンク->弱リンクとつないでいき最初のセルに戻るチェーンを探します。
最後だけは弱リンクでも構いません。そうすることによって、
[1]=強=>[1]=弱=>[1,1]=強=>[1]=弱=>[1]=強=>[1,1]=弱=>[1](OFFスタート)
[1]=強=>[1]=弱=>[?,?]=強=>[?]=弱=>[?]=強=>[1,1]=弱=>[1](ONスタート)
の2パターンが考えられいずれの場合も[1]を削除できるセルを探します。
最後のセル=最初のセルなのでONスタートの場合逆回りも考えます。最後のセルのとなりはOFFとなります。
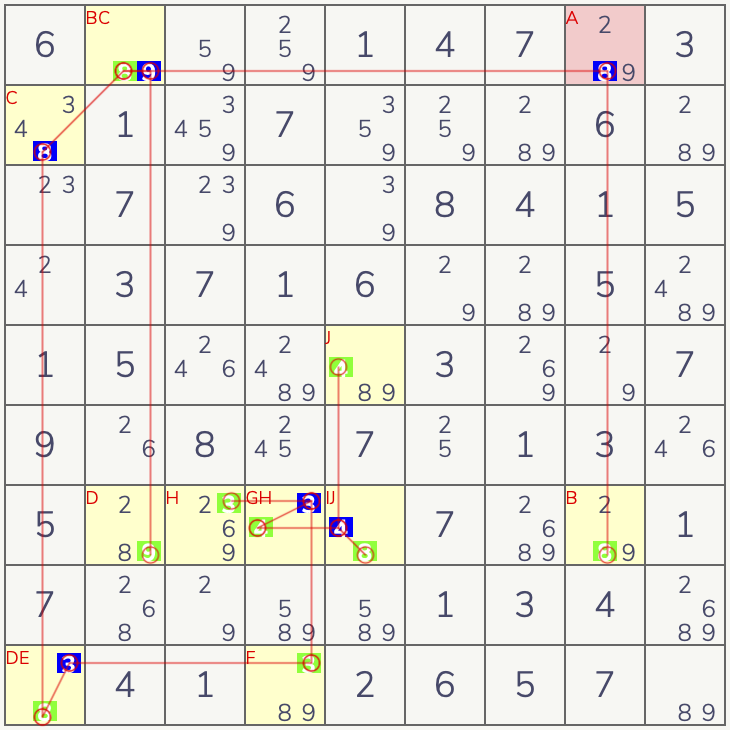
例:下図は[1]のグループXサイクルです。Xサイクル同様スタートに[1]が入らない場合チェーンがつながり1周します。
[R1C3]=強=>[R7C3]=弱=>[R7C7,R7C8]=強=>[R8C7]=弱=>[R3C7]=強=>[R3C1,R3C2]=弱=>[R1C3]で
スタートがOFFの時のONになるチェーン:[R7C3][R8C7][R3C1,R3C2]と
スタートONの時[R1C3]のどちらの場合も共通で削除できるセルが発生します。
問題を解くときはメモ機能を活用しましょう。
グループXサイクル
ABC...はチェーンの順番です。
いずれの場合も[R1C1][R1C2]には[1]は入れません
| 12 8 | 123 6 8 | 1 6 | 12 7 | 5 | 12 7 | 23 8 | 4 | 9 |
| 7 | 23 5 8 | 9 | 12 | 6 | 4 | 123 5 8 | 12 5 | 23 |
| 12 | 12 5 | 4 | 9 | 3 | 8 | 12 5 7 | 6 | 2 7 |
| 6 | 9 | 7 | 3 4 | 2 | 5 | 3 4 | 8 | 1 |
| 3 | 12 4 | 8 | 1 4 6 7 | 4 7 | 1 7 | 2 4 6 7 | 9 | 5 |
| 12 4 | 12 4 | 5 | 1 3 4 6 78 | 4 789 | 1 3 7 9 | 23 4 6 7 | 2 7 | 23 4 7 |
| 1 4 89 | 4 6 78 | 1 6 | 23 5 | 4 789 | 23 | 12 45 7 9 | 12 5 7 | 2 4 7 |
| 5 | 1 4 78 | 2 | 4 78 | 4 789 | 7 9 | 1 4 7 9 | 3 | 6 |
| 4 9 | 4 7 | 3 | 2 5 | 1 | 6 | 2 45 7 9 | 2 5 7 | 8 |
ルール2
Xサイクル・グループXサイクルどちらも最後は弱リンクでいいのですがもし強リンクでしかもチェーンの数が奇数の場合ルール2が成立します。
[1]=強=>[1]=弱=>[1,1]=強=>[1]=弱=>[1]=強=>[1,1]=弱=>[1]=強=>[1](OFFスタート)
最後のセル=最初のセルなので最初OFFでスタートしているにもかかわらず最後がONになってしまいます。
矛盾するので最初がOFFということにはならずに最初のセルは[ON]で確定します。
ルール3
Xサイクル・グループXサイクルどちらも最後は弱リンクでいいので、[弱]=>[弱]となる場合がでてきます。上と同様チェーンの数が奇数の場合で最後が[弱]=>[弱]の場合ルール3が成立します。
[1]=強=>[1]=弱=>[1,1]=強=>[1]=弱=>[1]=強=>[1,1]=弱=>[1]=弱=>[?](OFFスタート)
[1]=強=>[1]=弱=>[?,?]=強=>[?]=弱=>[?]=強=>[?,?]=弱=>[1]=弱=>[1](ONスタート)
最後のセル=最初のセルなのでONスタートの場合逆回りも考えます。最後のセルのとなりはOFFとなります。
OFFスタートでもONスタートでも[弱]=>[弱]で挟まれた最後のセルの1つまえは必ず[OFF]になります。
ソル君の考える解き方とは違う手順で解いたようです
思っているより早くセルの数字が確定しています。このまま進めていけばもしかしたらまたヒントが出せるようになるかもしれません。
(ソル君がいっているセルをクリアすればまたヒントを出すこともできます。)
エンプティレクタングル
文字より下の具体例の説明を最初に読んでもらった方がわかりやすいと思います。
9つのBOX単位に考えます。BOX内で縦横2本のラインが通っている時。[T]字か[L]字か[十]字の形になります。
例えば[1]のラインができているときBOX内では縦方向か横方向(あるいは両方)のどこかに[1]が来ます。そこまでは当たり前です。
どちらかの延長線上に[1]が入ると[1]が入れない2択のセル[X]があり、もう片方の延長線上に[1]が入ったセル[Z]があるとして、[X]と[Z]の交点に[X]の強リンクがあり[1]が入る時、[Z]から[1]を削除できます。
例:下図が具体例です。ピンクのセルが[9]のエンプティレクタングルです。
横のラインのどこかに[9]が来ると延長線上の[R3C7]のセルに[9]は入れず、強リンクの下の[R6C7]に[9]が入ります。ということは[R6C2]に[9]は入れません。
横のラインのどこかに[9]が来るとその真下の[R6C2]に[9]は入れません。
いずれにしても[R6C2]に[9]は入れないので削除することができます。※エンプティレクタングルはグループXサイクルでも解けます。
| 7 | 4 6 9 | 2 | 4 6 9 | 5 | 4 6 | 3 8 | 3 8 | 1 |
| 8 | 56 9 | 3 | 1 | 2 6 7 9 | 2 6 7 | 4 | 2 56 7 9 | 2 56 7 9 |
| 4 6 9 | 1 | 45 9 | 3 | 2 4 7 9 | 8 | 7 9 | 2 56 7 9 | 2 56 7 9 |
| 3 | 4 6 7 9 | 8 | 5 | 4 6 9 | 1 | 2 | 4 6 7 9 | 4 6 7 9 |
| 4 6 9 | 456 7 9 | 45 9 | 2 4 6 9 | 8 | 2 4 6 | 1 | 456 7 9 | 3 |
| 2 | 456 9 | 1 | 7 | 4 6 9 | 3 | 89 | 456 89 | 456 89 |
| 5 | 8 | 6 | 2 4 | 1 | 9 | 3 7 | 23 4 7 | 2 4 7 |
| 1 4 9 | 3 | 4 9 | 2 4 6 8 | 2 4 6 7 | 2 4 6 7 | 5 | 12 4 89 | 2 4 89 |
| 1 4 9 | 2 | 7 | 4 8 | 3 | 5 | 6 | 1 4 89 | 4 89 |
フィン付きX-ウィング
X-ウィングをベースにしたテクニックです。X-ウィングは4つの数字ですがそのうち1つが同じボックスで横(縦)ならびであっても使えるテクニックです。
X-ウィングは[左上][右下]と[右上][左下]が対になっていますが、フィン付きになるとどちらかが[1]対[BOX内の多]となります。
[1]対[1]のときと[1]対[BOX内の多]のとき共通して削除できる候補を消すことができるテクニックです。
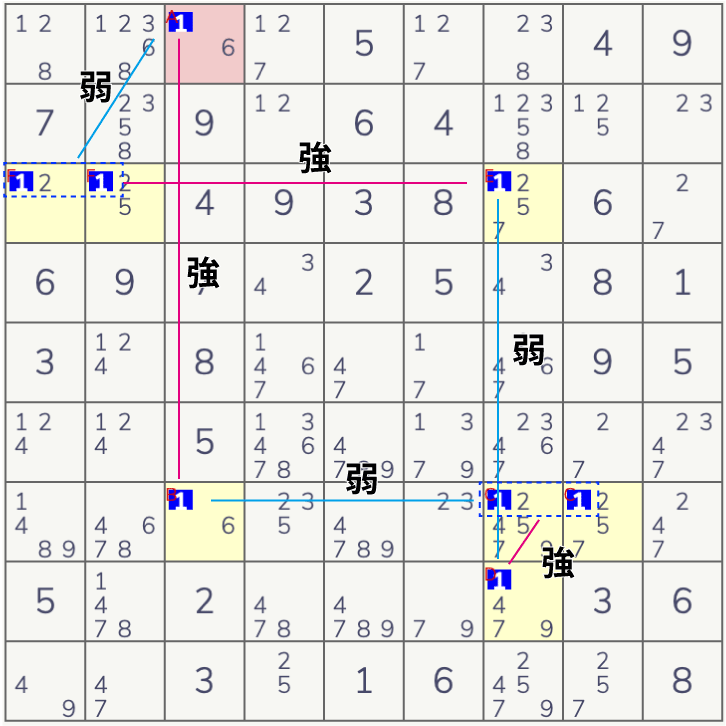
下図は具体例:[1]のフィン付きX-ウィングです。左上のピンクのセルに[1]が来ると必ず右下のピンクのセルは[1]になります。
右上のピンクのセルに[1]が来る場合が問題なのですが左下の黄色いセルのどこかに[1]が来ます。どちらにしても[R3C1]の[1]は入ることができません。左上に[1]が来たら同じ列で右下には[1]が来ないので左下の黄色いセルのどこかに[1]が来ます。ということは[R3C1]の[1]は同じBOX内なのでやはり入ることはできません。
| 12 5 7 9 | 12 | 1 7 9 | 1 7 9 | 45 9 | 1 45 7 9 | 3 | 8 | 6 |
| 1 8 | 6 | 4 | 2 | 3 | 1 8 | 7 | 9 | 5 |
| 5 789 | 5 9 | 3 | 789 | 5 89 | 6 | 2 | 4 | 1 |
| 123 9 | 7 | 5 | 1 3 89 | 4 89 | 1 4 89 | 1 6 8 | 1 3 6 | 23 4 8 |
| 6 | 1 3 4 | 1 89 | 1 3 789 | 2 | 1 4 789 | 5 | 1 3 | 3 4 8 |
| 123 | 123 4 | 1 8 | 5 | 6 | 1 4 8 | 9 | 7 | 23 4 8 |
| 5 7 9 | 5 9 | 6 7 9 | 4 | 1 | 2 | 6 8 | 3 56 | 3 8 |
| 4 | 8 | 2 | 6 9 | 5 9 | 3 | 1 6 | 1 56 | 7 |
| 1 3 5 | 1 3 | 1 6 | 6 8 | 7 | 5 8 | 4 | 2 | 9 |
フィン付きソードフィッシュ
フィン付きX-ウィングのソードフィッシュ版です。通常のソードフィッシュは3×3×3で探しますが、フィン付きは3×3×4でいけます。最後の1つ(フィン)は同じBOXにいることが条件です。
普通のソードフィッシュは3×3×3のどこかに対象の数字が入るため、列方向のソードフィッシュだと行方向のその数字を削除できます。
一方フィン付きソードフィッシュは最後のBOXでそこにその数字が来るかわかりません。しかしどちらかに入ることは間違い無いので、その場合BOX内の行方向の候補数字だけ削除できます。
下図が具体例です。[4]のソードフィッシュまでもう一歩なのですが水色のセルが余分です。右上に[4]が来なかった場合は右下BOX内のどちらかに[4]が来ます。
右上が[4]になった場合は三段目の左側2つのどちらかに[4]が来ます。どちらにしても[R7C9]の[4]は入ることができないため削除することができます。
| 5 | 6 | 1 4 7 | 9 | 1 4 | 1 4 7 | 8 | 3 | 2 |
| 12 4 7 | 9 | 8 | 1 4 6 | 3 | 12 45 7 | 45 7 | 6 7 | 456 7 |
| 2 4 7 | 3 | 2 4 7 | 8 | 2 456 | 2 45 7 | 1 | 9 | 456 7 |
| 3 | 7 | 1 4 | 2 | 1 4 8 | 1 4 8 | 6 | 5 | 9 |
| 12 4 6 | 2 4 | 5 | 1 4 6 | 1 4 6 7 | 9 | 3 | 2 7 | 8 |
| 2 6 9 | 8 | 2 6 9 | 5 | 6 7 | 3 | 2 7 | 4 | 1 |
| 6 78 | 2 4 | 3 | 1 4 | 9 | 12 45 8 | 45 7 | 12 6 7 | 456 7 |
| 2 4 9 | 1 | 2 4 9 | 7 | 2 45 | 6 | 2 45 | 8 | 3 |
| 6 78 | 5 | 6 7 | 3 | 12 4 8 | 12 4 8 | 9 | 12 6 7 | 4 6 7 |
AIC(オルタネーティング インファレンス チェーン)
X-サイクルの数字にこだわらない版です。X-サイクルは1つの数字でしたがAICでは数字が変わってもいいので強リンク・弱リンクで1周します。(図の下に説明)
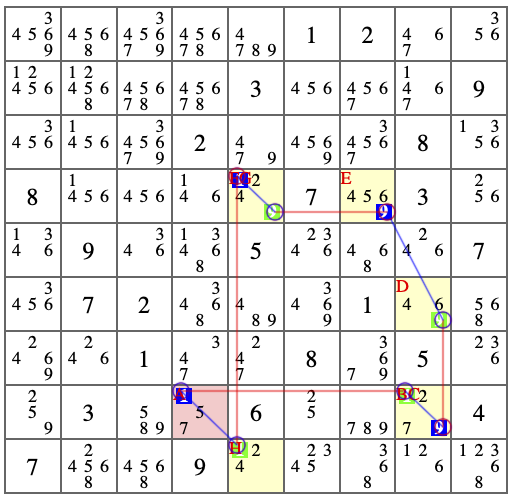
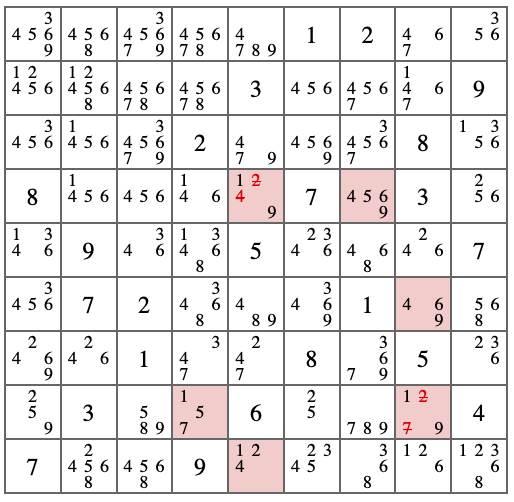
下図では[R8C4]=強=>[R8C8]=弱=>[R8C8]=強=>[R6C8]=弱=>[R4C7]=強=>[R4C5]=弱=>[R4C5]=強=>[R9C5]=弱=>[R8C4]でAICが成立しています。
(数字が変わるときはセル内で変わります)またチェーンの数が奇数ですので逆順に回しても数字が確定します。
下図は
[1]=強=>[1]=弱=>[9]=強=>[9]=弱=>[9]=強=>[9]=弱=>[1]=強=>[1]=弱=>[1]のチェーンです。
もしスタートがOFFならば
[1]=強=>[1]=弱=>[9]=強=>[9]=弱=>[9]=強=>[9]=弱=>[1]=強=>[1]=弱=>[1]となります。
もしスタートがONならば
[1]=強=>[?]=弱=>[?]=強=>[?]=弱=>[?]=強=>[?]=弱=>[?]=強=>[?]=弱=>[?]でわからなくなるのですが
逆回りに考えると
[1]<=強=[1]<=弱=[9]<=強=[9]<=弱=[9]<=強=[9]<=弱=[1]<=強=[1]<=弱=[1]となります
ということはどちらのチェーンになったとしても[R4C5]と[R8C8]は共通で入れない数字が出てきます。
問題を解くときはメモ機能を活用しましょう。
強リンク:行にその数字が2つしかない場合片方がその数字だともう片方にはその数字がはいりません。
| 2 6 7 | 456 | 45 7 | 8 | 2 7 | 9 | 4 6 7 | 3 | 1 |
弱リンク:行にその数字が3つ以上あると、1つに入らないことがわかっても、その数字がどこに入るかはわかりません。
| 6 7 | 1 | 4 7 | 2 | 8 | 4 6 7 | 9 | 5 | 3 |
しかし1つにその数字が決まると残りにその数字は入りません。入らないセルに別の強リンクがあればそちらにその数字は入ることになります。
| 6 7 | 1 | 4 7 | 2 | 8 | 4 6 7 | 9 | 5 | 3 |
ルール2
最後は弱リンクでいいのですがもし強リンクでしかもチェーンの数が奇数の場合ルール2が成立します。
[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=強=>[1](OFFスタート)
最後のセル=最初のセルなので最初OFFでスタートしているにもかかわらず最後がONになってしまいます。
矛盾するので最初がOFFということにはならずに最初のセルは[ON]で確定します。
ルール3
最後は弱リンクでいいので、[弱]=>[弱]となる場合がでてきます。上と同様チェーンの数が奇数の場合で最後が[弱]=>[弱]の場合ルール3が成立します。
[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=強=>[1]=弱=>[1]=弱=>[?](OFFスタート)
[1]=強=>[1]=弱=>[?]=強=>[?]=弱=>[?]=強=>[?]=弱=>[1]=弱=>[1](ONスタート)
最後のセル=最初のセルなのでONスタートの場合逆回りも考えます。最後のセルのとなりはOFFとなります。
OFFスタートでもONスタートでも[弱]=>[弱]で挟まれた最後のセルの1つまえは必ず[OFF]になります。
スゥ-ド-ク
ボックス内の同じ行か列にある2つのセルで候補が合計4つ。同じボックス内の他のセルで4つの候補のうち2つの候補のセル。ボックス外の行か列の延長上に残りの候補2つで成立します。
下図を見るとピンクのペアのセルに[1,2,3,6]の4つの候補。ボックス内のはみ出したセルに[1,3]、縦のライン状のボックス外、水色のセルには[2,6]があります。
黄色いセルは[1,3]ですが[1]になったとすると、ピンクのペアのセルと水色のセルで[2,3,6]のネイキッドトリプル(三国同盟)が成立します。[3]になったとすると、ピンクのペアのセルと水色のセルで[1,3,6]のネイキッドトリプル(三国同盟)が成立し、どっちにしてもライン状には[3,6]は入ることができません。
次に水色のセルは[2,6]です。こちらも[2]になったとするとピンクと黄色のセルで[1,3,6]、[6]だと[1,2,3]のネイキッドトリプル(三国同盟)です。ボックス内に[1,3]は入ることができません。
| 8 | 12 6 | 12 4 6 7 | 2 5 7 | 3 | 2 45 9 | 2 9 | 2 5 7 9 | 1 6 |
| 2 7 | 5 | 1 3 | 6 | 2 789 | 2 89 | 4 | 2 7 9 | 1 3 |
| 2 4 6 7 | 23 6 | 9 | 2 45 7 | 2 4 7 | 1 | 8 | 2 5 7 | 3 6 |
| 3 | 12 9 | 12 45 | 12 5 | 2 9 | 2 45 9 | 6 | 8 | 7 |
| 2 4 6 | 2 6 | 8 | 3 | 2 4 | 7 | 5 | 1 | 9 |
| 5 9 | 7 | 1 5 | 1 5 8 | 6 | 5 89 | 3 | 4 | 2 |
| 1 | 2 89 | 2 7 | 2 4 78 | 2 4 78 | 3 | 2 9 | 6 | 5 |
| 2 6 7 9 | 3 6 89 | 23 6 7 | 2 78 | 5 | 2 6 8 | 1 | 2 9 | 4 |
| 2 56 | 4 | 2 56 | 9 | 1 | 2 6 | 7 | 3 | 8 |
ディジット フォーシングチェーン
フォーシングチェーン(強制連鎖)の第一弾です。
一つのセルの一つの数字に注目。ONとOFFの2つのチェーンを作ります。(弱リンクも考慮に入れる)
2つのチェーンで共通で削除できる候補を削除することができます。
もし1セルにONでもOFFでも入った場合はそれ以外の数字を削除でます。ほかにもパターンがあり下図にまとめます。
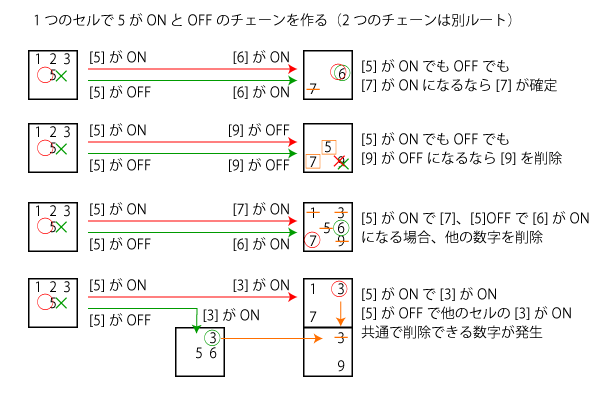
具体例は下図のようになります。オリジナル例が難しくて作れませんでした。引用SudokuWiki.org
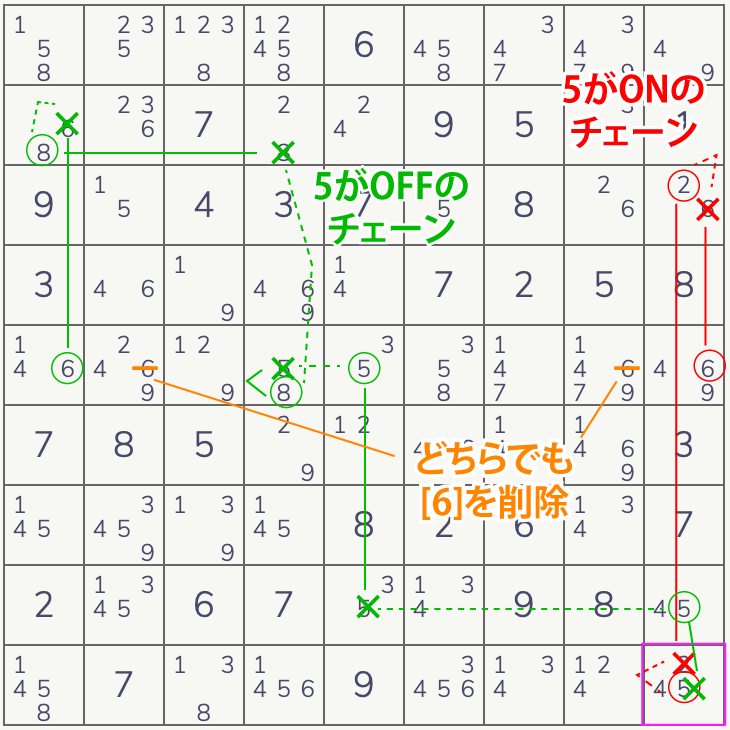
AICの一周しない版となります。一周しなくていいので幅広くなりますが難易度が高いテクニックで優先順位も下がるので実際にはほかのチェーンで解けてしまいます。サンプル問題もいちおうディジット フォーシングチェーンを使う機会はでてくるのですが、実際には使わず解けてしまいます。
西尾フォーシングチェーン
フォーシングチェーン(強制連鎖)の第二弾です。
ナンプレ上級者の間で絶大な支持を受けるパズル作家、西尾徹也氏のテクニックです。
テクニック自体も非常に強力でなんでも解いてしまうような勢いです。
一つのセルの一つの数字に注目。ONのチェーンを2つ作ります。(弱リンクも考慮に入れる)
2つのチェーンで矛盾した場合その候補はなしということになります。
逆にOFFのチェーンで矛盾する場合は確定ということになります。
矛盾のパターンがいくつかあり下図にまとめます。
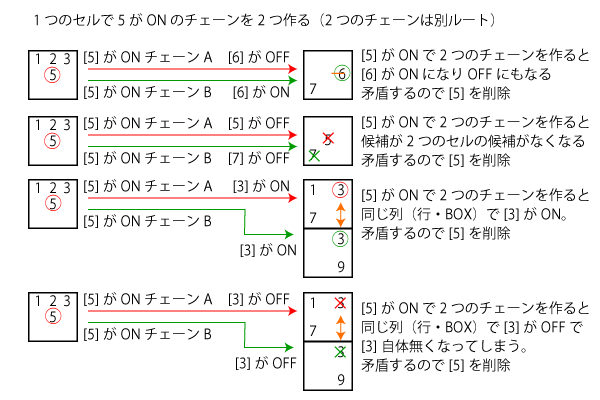
具体例は下図のようになります。オリジナル例が難しくて作れませんでした。引用SudokuWiki.org
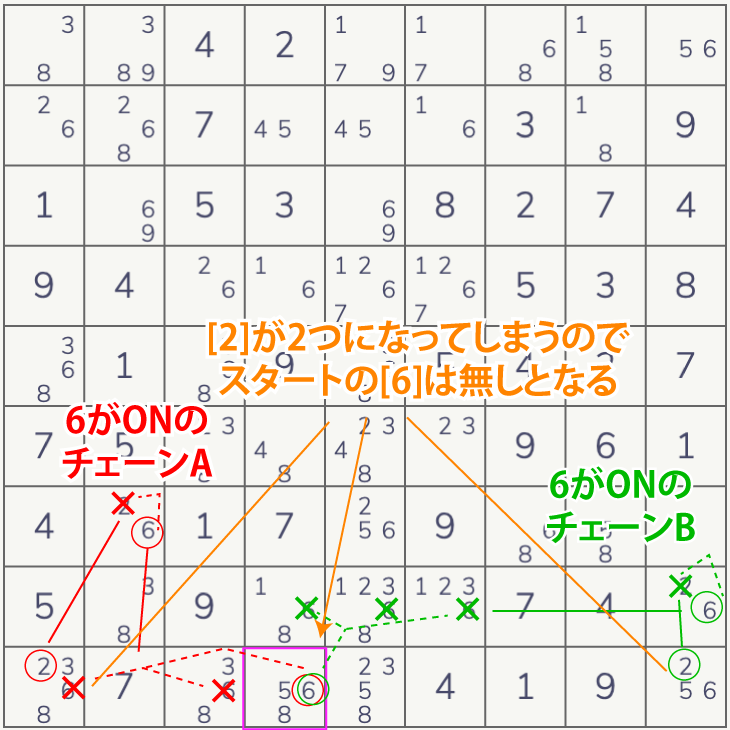
AICの一周しない版となります。難易度が高いテクニックなのですがナンプレラボではチェーンの長さに制限をかけていないのでとんでもない解き方になったりします。サンプル問題もいちおう西尾フォーシングチェーンを使う機会はでてくるのですが、実際には使わず解けてしまいます。
セルフォーシングチェーン
フォーシングチェーン(強制連鎖)の第三弾です。
3択から4択のセルに注目。候補の数だけONのチェーンを作ります。(弱リンクも考慮に入れる)
ディジットフォーシングチェーンと同じで全てのチェーンで共通で削除できる候補を削除することができます。
もし1セルに全てのチェーンで候補が入った場合はそれ以外の数字を削除でます。ほかにもパターンがあり下図にまとめます。
ちなみに2択だと1つの数字のON・OFFでチェーンを作るディジットフォーシングチェーンと同じとなります。
さらに4択の場合はクアッドフォーシングチェーンというようです。
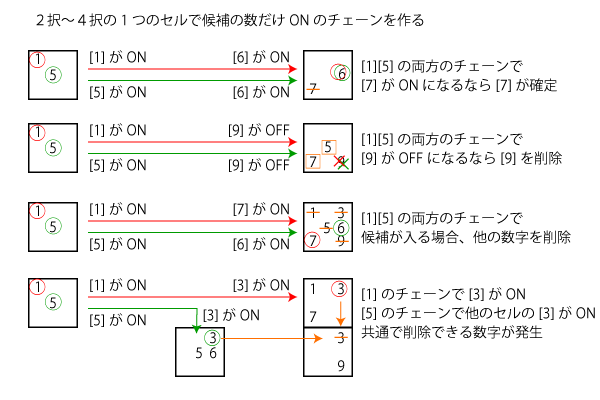
具体例は下図のようになります。オリジナル例が難しくて作れませんでした。引用SudokuWiki.org
このテクニックもほかの強制連鎖と同様に他のテクニックで解けてしまうことが多いです。サンプル問題もいちおうセルフォーシングチェーンを使う機会はでてくるのですが、実際には使わず解けてしまいます。
ユニット フォーシング チェーン
フォーシングチェーン(強制連鎖)の第四弾です。
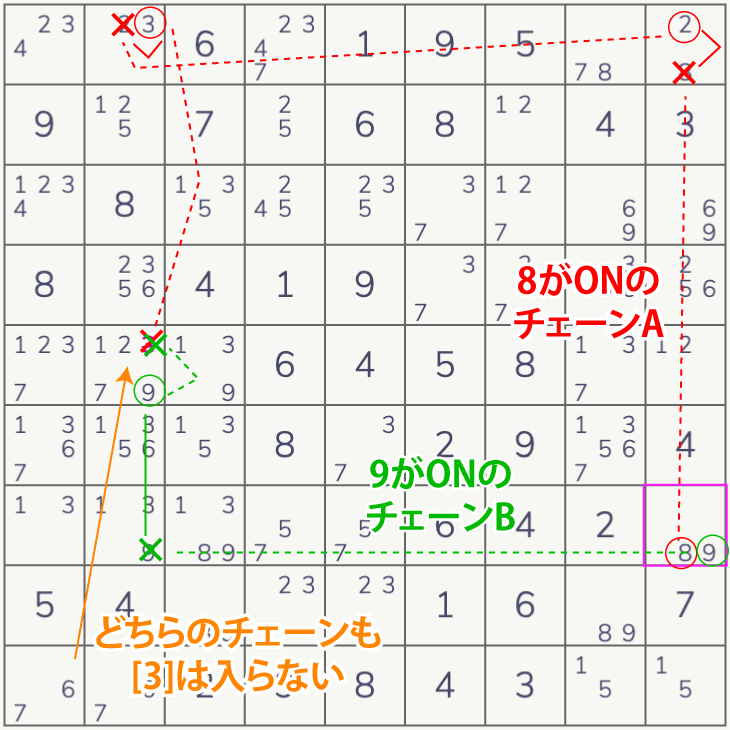
行・列・BOXに2から4つしかない候補に注目します。それらの全てにチェーンを作ります。
あとはディジットフォーシングチェーンと同じで全てのチェーンで共通で削除できる候補を削除することができます。
もし1セルに全てのチェーンで候補が入った場合はそれ以外の数字を削除でます。ほかのパターンもディジットフォーシングチェーンと同じです。
実はチェーンは全部作らなくてもよく、1つはその数字で確定と考えて残りのチェーンで共通の削除候補を探してもOKです。
具体例は下図のようになります。オリジナル例が難しくて作れませんでした。引用SudokuWiki.org
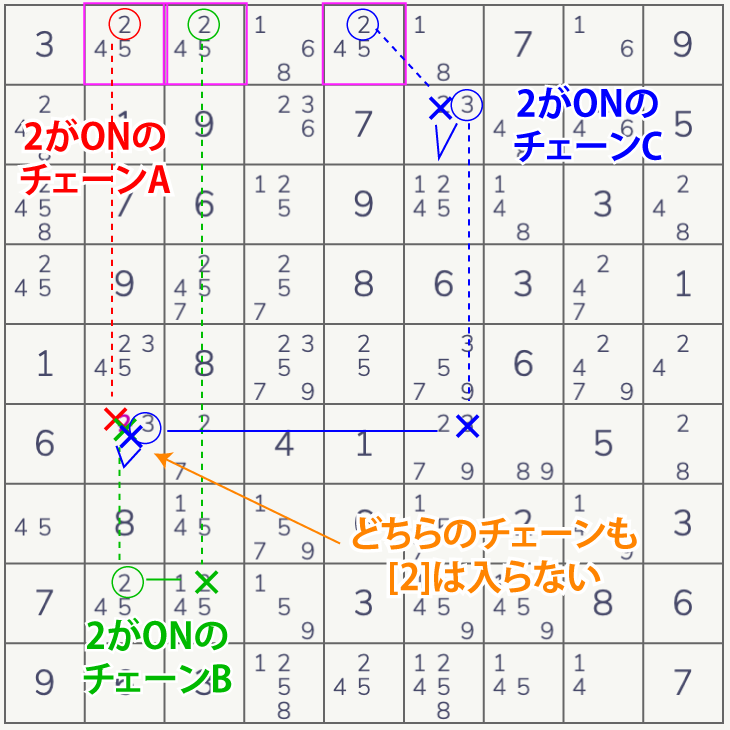
このテクニックもほかの強制連鎖と同様に他のテクニックで解けてしまうことが多いです。サンプル問題もいちおうセルフォーシングチェーンを使う機会はでてくるのですが、実際には使わず解けてしまいます。
ALS ほぼロックされたセット
セルの数+1の候補数をほぼロックされた状態といいます。n+1という言い方をよくするのですが、例えばセル2つで[1,3][1,3,4]なら候補数は3でほぼロックされた状態です。
ALSはこのほぼロックされた状態の組み合わせが2つあって、それぞれの組み合わせで1回しか出ない共通の数字の候補を持ち、その候補は互いに影響している状態です。
図では[2,4][1,4]の組み合わせ(黄色)と[2,9][1,9]の組み合わせ(ピンク)がそうです。共通候補[1]はどちらの組み合わせにも1回だけ登場しお互いに影響しあっています。(候補[X]という)。
黄色の方に[1]が来るとピンクには[1]は使えなくなってネイキッドペアになります。逆にピンクの方に[1]が来ると黄色には[1]は使えなくなってやはりネイキッドペアです。
それぞれで確定する[2]ですが(候補[Z]という)必ずどちらかが[2]になります。そして、どちらになったとしても[R1C6]の[2]は入れることができません。
| 8 | 6 | 2 4 | 1 | 23 45 | 23 5 9 | 45 9 | 3 5 9 | 7 |
| 1 3 4 | 9 | 5 | 6 | 7 | 8 | 1 4 | 1 3 | 2 |
| 1 3 4 | 7 | 12 4 | 4 9 | 23 45 | 23 5 9 | 8 | 6 | 1 45 9 |
| 6 | 12 45 | 7 | 23 | 9 | 3 5 | 1 45 | 8 | 1 45 |
| 9 | 2 5 | 8 | 2 5 | 1 | 4 | 6 | 7 | 3 |
| 1 4 | 1 45 | 3 | 7 | 8 | 6 | 1 45 9 | 2 | 1 45 9 |
| 7 | 8 | 9 | 3 5 | 3 56 | 1 | 2 | 4 | 56 |
| 5 | 3 | 1 4 | 8 | 2 4 6 | 2 9 | 7 | 1 9 | 1 6 9 |
| 2 | 1 4 | 6 | 4 9 | 45 | 7 | 3 | 1 5 9 | 8 |
この例の共通候補[1]はどちらにも来ないこともありえるが、その場合でも成立している
デスブロッサム
あと1つでネイキッドペア・トリプル・クアッドになるようなALSが2つあり、その2つを2択のセルでつなぐというテクニックです。
下図でピンクはセルが2つで候補数字が[4,5,8]のように3つなら(セルの数+1)ほぼロックされたセットALSです。
また黄色はセルが2つで候補数字が[1,4,7]のように3つのALSです。これを水色の2択セル[1,5]があり、この2択は2つのALSに繋がっています。
水色が[1]だと黄色は[4,7]のネイキッドペアになり、水色が[5]の場合はピンクは[4,8]で確定です。水色が[1]でも[5]でも[R9C8]に[4]は入れません。
※ALSはAlmost Locked Set:ほぼロックされたセットの意味です。
| 2 45 8 | 9 | 6 | 23 45 | 1 5 | 123 45 | 45 78 | 1 4 7 | 45 78 |
| 3 | 45 | 1 | 8 | 56 9 | 7 | 456 9 | 2 | 45 9 |
| 2 45 8 | 45 7 | 2 4 78 | 2 456 | 1 56 9 | 12 45 | 456 89 | 1 4 6 9 | 3 |
| 9 | 3 | 2 4 7 | 2 6 7 | 6 78 | 2 8 | 1 | 5 | 2 4 |
| 1 | 4 6 7 | 2 4 7 | 2 5 7 | 3 | 2 5 9 | 4 6 9 | 8 | 2 4 9 |
| 2 6 | 8 | 5 | 1 | 4 | 2 9 | 3 6 7 9 | 3 6 7 9 | 2 7 9 |
| 45 8 | 1 45 | 9 | 3 45 7 | 1 5 78 | 1 3 45 8 | 2 | 4 7 | 6 |
| 456 8 | 1 456 | 3 | 45 7 | 2 | 1 45 8 | 45 789 | 4 7 9 | 5 789 |
| 7 | 2 | 4 8 | 9 | 5 8 | 6 | 3 45 8 | 3 4 | 1 |
パターンオーバーレイメソッド
[3]なら[3]というように特定の数字に絞って、それの全パターンを洗い出します。
強リンクの組み合わせで目星をつけて仮置きする感じですね。チェーンに似ていますがチェーンよりわかりやすいかもしれません。
序盤でするとパターンが多くなりすぎるので中盤ぐらいで使うテクニックです。
下図で[4]をみてみます。一番下の行が2択になっているのでここを起点にすべてのパターンを出します。
| 2 9 | 8 | 2 9 | 1 | 6 | 3 | 4 | 7 | 5 |
| 1 7 | 4 | 1 7 | 9 | 8 | 5 | 6 | 2 | 3 |
| 5 | 3 | 6 | 7 | 2 | 4 | 1 | 9 | 8 |
| 8 | 6 | 1 45 | 45 | 3 | 2 | 9 | 1 45 | 7 |
| 1 4 9 | 2 | 1 45 9 | 8 | 1 45 | 7 | 3 | 6 | 1 4 |
| 3 | 7 | 1 45 | 6 | 1 45 | 9 | 8 | 1 45 | 2 |
| 2 4 | 9 | 8 | 23 45 | 45 | 6 | 7 | 1 3 4 | 1 4 |
| 2 4 7 | 1 | 23 4 7 | 23 4 | 9 | 8 | 5 | 3 4 | 6 |
| 6 | 5 | 3 4 | 3 4 | 7 | 1 | 2 | 8 | 9 |
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
4
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
4
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
4
4
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
4
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
4
0
4
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
4
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
4
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
4
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
4
4
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
4
0
0
0
0
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
4
0
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
どのパターンになったとしても入らない[4]があります。その[4]は削除が可能です。またどのパターンでも候補が[4]になるセルがあればそれは確定となります。
| 2 9 | 8 | 2 9 | 1 | 6 | 3 | 4 | 7 | 5 |
| 1 7 | 4 | 1 7 | 9 | 8 | 5 | 6 | 2 | 3 |
| 5 | 3 | 6 | 7 | 2 | 4 | 1 | 9 | 8 |
| 8 | 6 | 1 45 | 45 | 3 | 2 | 9 | 1 45 | 7 |
| 1 4 9 | 2 | 1 45 9 | 8 | 1 45 | 7 | 3 | 6 | 1 4 |
| 3 | 7 | 1 45 | 6 | 1 45 | 9 | 8 | 1 45 | 2 |
| 2 4 | 9 | 8 | 23 45 | 45 | 6 | 7 | 1 3 4 | 1 4 |
| 2 4 7 | 1 | 23 4 7 | 23 4 | 9 | 8 | 5 | 3 4 | 6 |
| 6 | 5 | 3 4 | 3 4 | 7 | 1 | 2 | 8 | 9 |