

Sponsored Links
Sudoku Tricks
We've collected some useful tricks for solving the puzzles in one easy place. As there are some which are hard to understand, we've tried to explain them simply. Paired Cells
Paired Cells
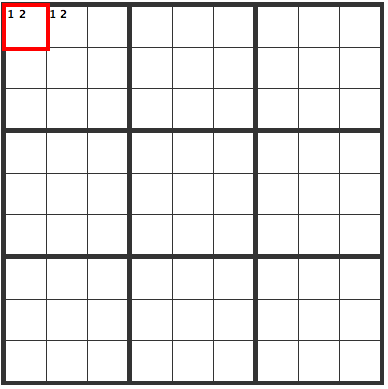
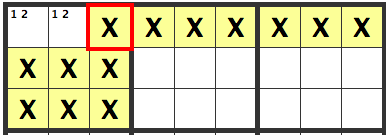
In the upper left, we've created a pair of cells marked "1 2". In this situation, the upper left could either be 1, 2 or 2, 1 so the following "X" cells can't contain a 1 or a 2.
Trio of Cells
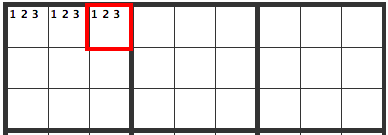
Just as you could have paired cells, you could have a trio of cells. In this situation, the upper left cells have 1, 2, and 3 in them, so they can't go in any other cells in that box. This goes for the box, as well as for cells across from or below.
Four Cells
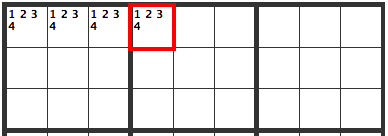
You could also have four cells. In this situation, the upper left cells have 1, 2, 3, and 4 in them, so they can't go in any other cells in that box. This goes for the box, as well as for cells across from or below.
When Potential Cells are in a Line
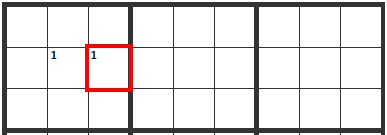
When a 1 is limited to two cells in the same row, the following "X" cells can't contain a 1.
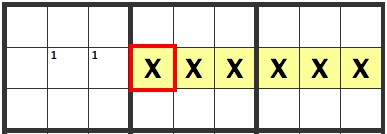
When Potential Cells are in a Square
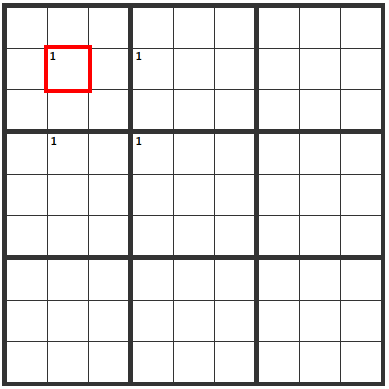
This is known as the x-wing. If this situation occurs, whether the cells are
1
1
or
1
1
the following "X" cells can't contain a 1.
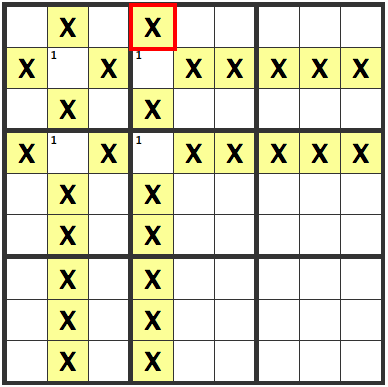
When there are 9 Potential Cells Lined up
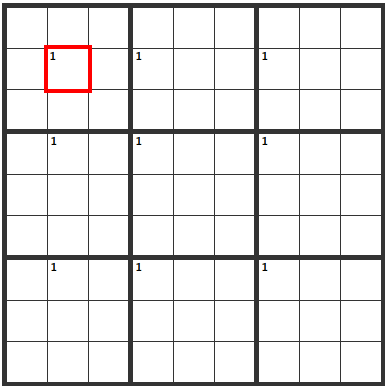
This is the same situation as above, only with 9 cells. The following "X" cells can't contain a 1.
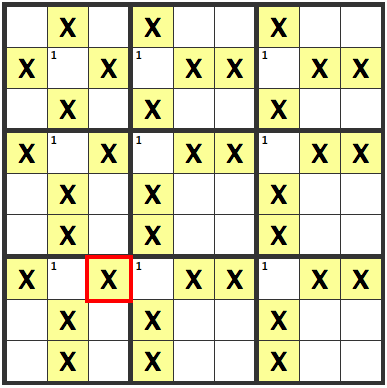
The Following Situation
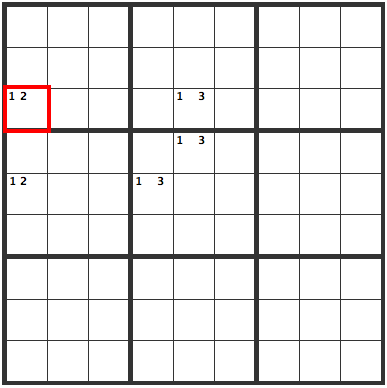
This is known as "Hamada Logic". Since the cells marked "1 2" on the left contain either a 1 or a 2, of the three cells marked "1 3", 1 is left in the column not under the influence of the "1 2" cells.
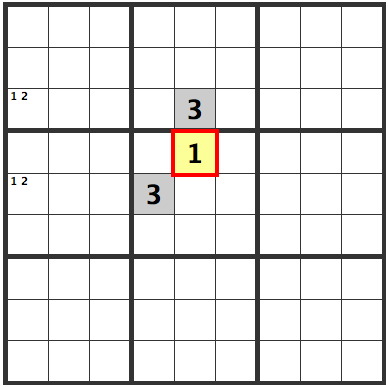
Why you ask? If, conversely we had
1
3
1
then the "1 2" cells on the left could not hold true.
Sponsored Links
Three-way Deadlock Pattern
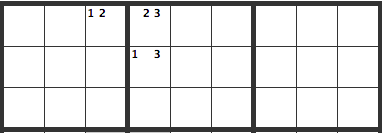
This sort of pattern can exist. In this instance, a 1 or a 2 can go in the upper left cell marked "1 2".
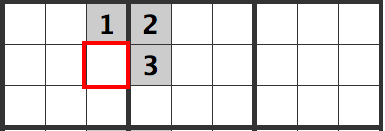
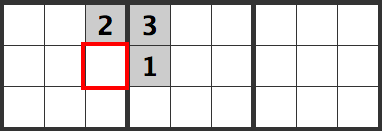
In either case, a 1 cannot go into the cell below it.
Underhanded
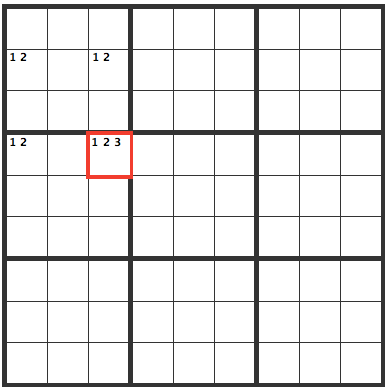
In a situation such as this, the red cell is a 3.
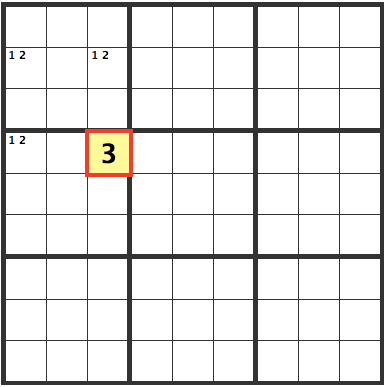
If it were a 1 or a 2,
1 2
2 1
or
2 1
1 2
would both be valid, giving multiple solutions, meaning it wouldn't be a valid sudoku puzzle.
Sponsored Links

