

Sponsored Links
TOP > Techniques > Naked Pairs/Triples/Quads
Solving Techniques 2
Naked Pairs/Triples/Quads
When a pair like [1,2] [1,2] exists, this technique allows for the elimination of [1,2] as candidates from other cells.
Naked Pairs
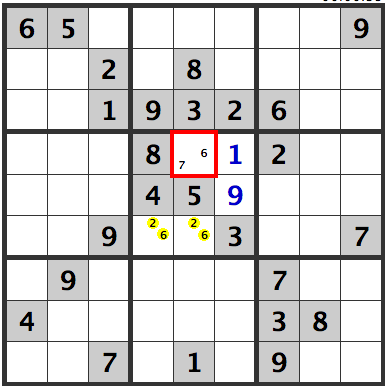
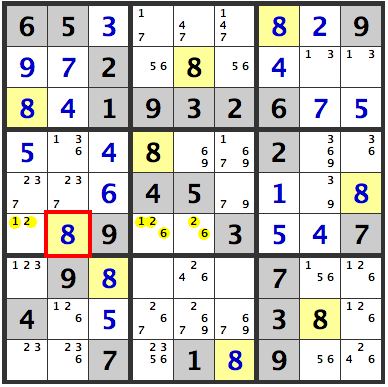
The candidates for the center box are [2,6 and 7]. However, since there is already a 7 in row [6], at [R6C9], a pair of [2,6][2,6] arises. Hence, [2 or 6] can't be entered at [R4C5], confirming that a 7 is in this cell.
In the example below, too, a [2,3] pair arises between [R7C1] and [R9C1], in the lower left box. Hence, a 2 or 3 can't be in the other cells of this box. Therefore, a [6] goes in [R9C2] and at the same time a [1] is confirmed for [R8C2].
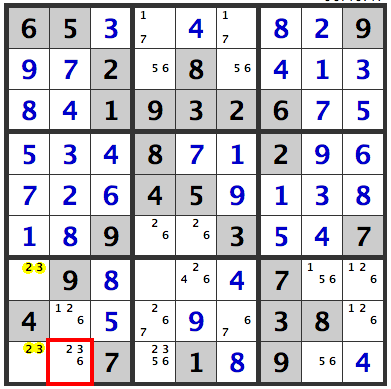
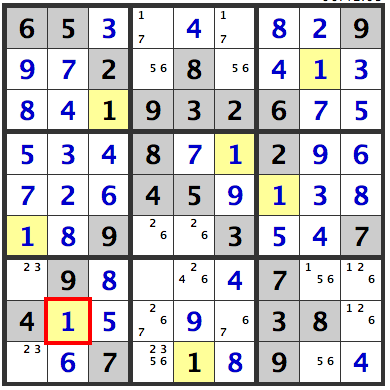
Naked Triples
Lets examine row [6]. Between [R6C1]:[1,2], [R6C4]:[1,2,6], and [R6C5]:[2,6] a triple of 1, 2, 6 arises. In these cells, a 1, 2 or 6 will be entered, eliminating the possibility of having these numbers in other cells in the same row. Hence, an [8] at [R6C2] is confirmed.
{3,3,3} of [1,2,3][1,2,3][1,2,3] ,
{3,3,2} of [1,2,3][1,2,3][1,2],
{3,2,2} of [1,2,3][1,2][2,3],
and {2,2,2} of [1,2][2,3][1,3],
are all types of triples that will work out.
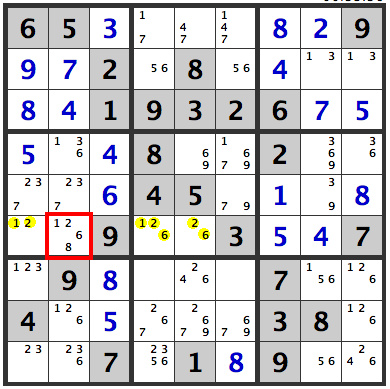
Sponsored Links
Naked Quads
The same can be applied to patterns of 4.
Naked Pairs/Triples/Quads is also a basic problem solving technique for Sudoku.
The fewer the hints, the more candidates there will be for the cells, and there will be many naked patterns that will arise. Pairs are easy, but triples and quads occur not just with the same three or four numbers, but also work when there are not enough numbers, so they are trickier to find. Once you start looking for these patterns, the problems will become much easier to solve.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links

