

Sponsored Links
TOP > Techniques > Extended Unique Rect.
Solving Techniques 16
Extended Unique Rect.
This is a three-cell version of the Unique Rectangles.
In the diagram below, either [123][231][312] or [312][123][231] would work as solutions.
We presume that a Sudoku problem can’t have two solutions.
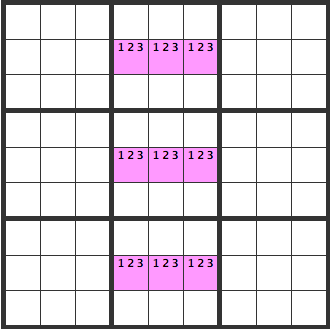
The diagram below examines how many combinations of [123] there are. There are 12 patterns that have multiple solutions.

Also, [123][123][23] or [12][123][123] or [123][12][23] are extended unique rectangles.
Further, [12][23][13] are also extended unique rectangles.

Extended Unique Rect. 1
In the diagram below, the yellow part becomes [8][9]. Otherwise, we have an extended unique rectangle, which has multiple solutions.
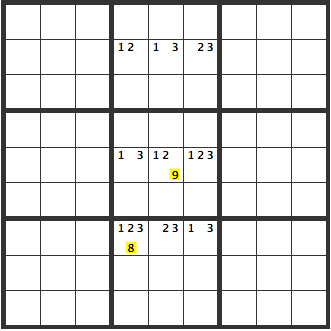
Lets examine below. If the solution only contained the red 8, the other cells will become the yellow candidates, creating an extended unique rectangles.
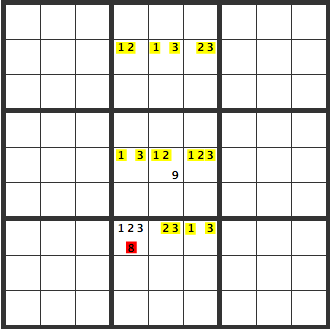
If, as below, only the red [9] was in the solution, then too, the other cells will become the yellow candidates, creating an extended unique rectangles. Therefore, [8][9] are both confirmed. (Otherwise, we are left with multiple solutions)
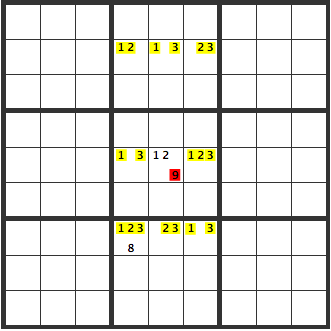
Sponsored Links
Extended Unique Rect. 2
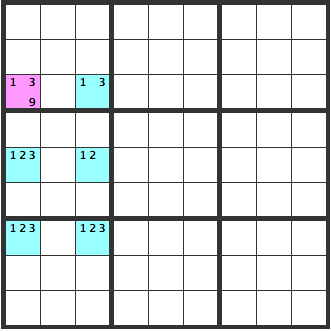
The pink [139] cell will be a [9].
Extended Unique Rect. 3
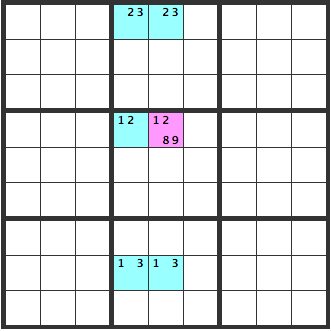
The pink [1289] cell will be [8] or [9].
Extended Unique Rect. 4
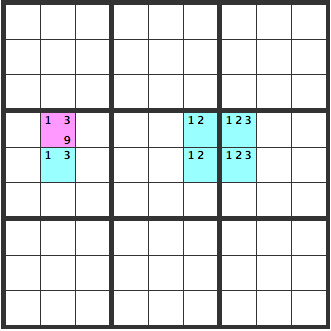
The pink [139] cell will be a [9].
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links

