 文章:
文章:DTP関連のIT技術者。システム開発など
運営:嵐山デザインガレージ合同会社たけうちとおるのスクリプトノート| ファイナンシャルプランナー| 著書(Amazon)


スポンサーリンク
無料で遊べる数独サイト「ナンプレ京」がお届けする、超上級者向け知的挑戦。“3Dメデューサ(3D Medusa)”という名の技法は、1数字だけに注目せず、複数数字を絡めた“色付き連鎖”を使って候補を削除する革新的な手筋です。和の静けさと洗練された演出の中で、解き筋を極める時間をお楽しみください。
3Dメデューサ
片方に入ったらもう片方には入らない強リンクで全て繋いでいきます。数字はなんでもいいです。
そうするとメデューサ髪の毛のようにチェーンがからまりあった状態になります。ここでON/OFFの2つのチェーンを色つけします。
ルール1片方のチェーンが1つのセルに2つの候補が正解になってしまう(例:ONの場合[1,8]が同セルに入る):矛盾したらその色は全部削除です。
ルール2片方のチェーンが行列BOXで候補が重なってしまう(例:OFFの場合8が同じ行2つできる):矛盾したらその色は全部削除です。
ルール32つのチェーンのどちらでも1つのセルに候補が入る(例:セルA[1,6,8]にON[1]OFF[8]だと[6]は削除):その候補以外は削除できます
ルール42つのチェーンのどちらでも共通で削除できる候補(例:ONの場合[R1C1]に[1]、OFFの場合[R1C9]に[1]なら他の[R1]の[1]は全て削除):その候補は削除できます
ルール52つのチェーンのどちらでも共通で削除できる候補(例:ONの場合セルA[1,6]に[1]、OFFの場合その隣のセルが[6]ならセルAに[6]は入れない):その候補は削除できます
ルール6片方のチェーンの場合空白になるセルができてしまう(例:ONの場合セルAに[1]、セルBに[5]、セルABの延長に[2,5]のセルがあるとONの場合[2,5]はなくなってしまう):矛盾したらその色は全部削除です。
例:下図がルール2の具体例です。[R1C8]に[8]を入れない場合、行7に8が複数確定します。矛盾するので[R1C8]は[8]になります。
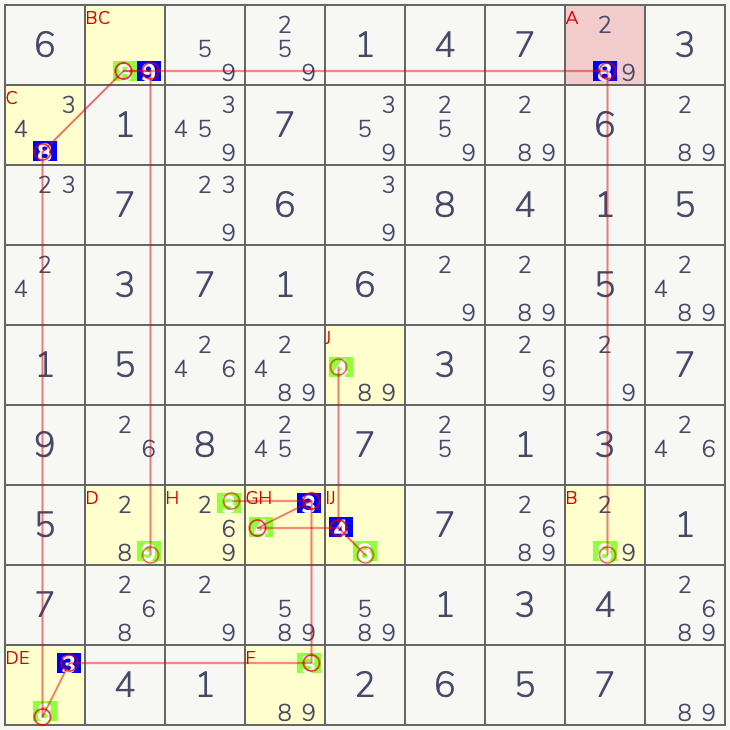
かなり難しい3Dメデューサ。その分強力でかなりの難問がこのテクニックで解けてしまいます。
あまりにも強力なのでプログラムの開発中はOFFにして作ったりしました。(そうしないと解いてしまう)
プログラムでチェーンを作るのが難しくてこれの開発で10日ぐらいかかりました。
名前がかっこよく思い入れのある解き方です。強リンクでチェーンを作るだけなのですが正直使いこなせるとは思えません。そもそも仮置きみたいな物でもあると思います。
シングルチェーンに似てるけど数字はこだわらず・XYチェーンにてるけど弱リンクは考えません
3Dメデューサがおかしいのでは無いかというご指摘を受けソースを見直し作り直しました。ルール5・6も解けるようになりました
ルール1
[R1C2]に[1]を入れると[R4C9]に2つの数字が確定してしまいます。
ABCは順番でAから派生する数字が2つあればBも2つある
| 8 | A 1 6 | B 1 6 | 4 | 3 | 7 | 5 | 9 | 2 |
| 4 | 3 | 2 | 9 | 8 | 5 | 6 | 1 | 7 |
| 5 9 | 5 9 | 7 | 1 | 2 | 6 | 8 | 4 | 3 |
| 12 7 9 | 12 4 7 9 | 8 | 2 7 | 5 | 2 4 | 3 | 6 | 1 4 9 |
| 6 | 12 4 7 | 1 4 | 23 7 | 9 | 23 4 | 12 4 | 5 | 8 |
| 3 | 2 45 9 | 45 | 8 | 6 | 1 | 2 4 | 7 | 4 9 |
| 12 5 | 12 45 | 9 | 23 5 | 7 | 23 | 1 4 | 8 | 6 |
| 2 5 | 8 | F 456 | 2 56 | 1 | 9 | 7 | 3 | E 45 |
C 1 5 7 | B 56 7 | 3 | 56 | 4 | 8 | 9 | 2 | D 1 5 |
ルール3
[R1C1]に[1,7]どちらを入れても共通して候補が入るセルから候補外の数字を削除。
(例:[1234]が候補のセルで、最初のセルが[1]の場合[1]になり、最初のセルが[7]の場合[3]になるとすると、いずれの場合でも[24]は入らない)
(チェーンの色が2色入っているセルは色がついていない数字は省ける)
->:[R7C1]の候補5を削除
[R1C1]に[1]の場合[R7C1]は[4]になる。
A 1 7 | 9 | 4 | 23 | 6 | 23 | 8 | 5 | B 1 7 |
| 3 | 2 | 5 | 7 | 1 | 8 | 4 9 | 4 9 | 6 |
| 6 | E 1 8 | D 78 | 4 | 5 9 | 5 9 | C 1 7 | 2 | 3 |
| 9 | 5 8 | 6 | 12 5 8 | 2 45 8 | 2 45 | 12 7 | 3 | 12 78 |
| 2 | 3 | 1 | 6 | 89 | 7 | 5 | 89 | 4 |
| 5 7 | 4 | E 78 | 123 5 89 | 23 5 89 | 23 5 9 | 12 9 | 6 | 12 8 |
| 1 45 | F 1 56 | 9 | 2 5 8 | 7 | 2 456 | 3 | 4 8 | 2 5 8 |
| 8 | 56 | 2 | 3 5 | 3 45 | 1 | 4 6 | 7 | 9 |
| 45 | 7 | 3 | 2 5 89 | 2 45 89 | 2 456 9 | 2 6 | 1 | 2 5 8 |
[R1C1]に[7]の場合[R7C1]は[1]になる。
A 1 7 | 9 | 4 | 23 | 6 | 23 | 8 | 5 | B 1 7 |
| 3 | 2 | 5 | 7 | 1 | 8 | 4 9 | 4 9 | 6 |
| 6 | D 1 8 | E 78 | 4 | 5 9 | 5 9 | C 1 7 | 2 | 3 |
| 9 | E 5 8 | 6 | 12 5 8 | 2 45 8 | 2 45 | 12 7 | 3 | 12 78 |
| 2 | 3 | 1 | 6 | 89 | 7 | 5 | 89 | 4 |
F 5 7 | 4 | F 78 | 123 5 89 | 23 5 89 | 23 5 9 | 12 9 | 6 | 12 8 |
B 1 45 | 1 56 | 9 | 2 5 8 | 7 | 2 456 | 3 | 4 8 | 2 5 8 |
| 8 | 56 | 2 | 3 5 | 3 45 | 1 | 4 6 | 7 | 9 |
| 45 | 7 | 3 | 2 5 89 | 2 45 89 | 2 456 9 | 2 6 | 1 | 2 5 8 |
いずれの場合でも[5]は入らない
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Rは行(Y軸)、Cは列(X軸)となっています。(Row、Column)
 文章:
文章:DTP関連のIT技術者。システム開発など
運営:嵐山デザインガレージ合同会社