

ナンプレ京 交流掲示板
ログイン会員様限定で発言できる掲示板です。交流掲示板なので仲良くやさしくお願いいたします。
PCのみプッシュ通知に対応しました。新しい投稿があった時に通知されます。プッシュ通知を許可する(新しくウィンドウが開くのでそのウィンドウでプッシュ通知を許可してください)

[2437]マイトピア (2026-03-06 05:43:07)
もうパンツは見飽きたよ

[2436]管理人 (2026-02-18 11:26:41)
ご連絡ありがとうごいます
>[閉じる]ボタンが見当たらない全画面広告がPLAY中にも表示されるようになりました。
プレイ画面は除外設定していたのですが
いつのまにか設定が消えていました。反映に時間がかかるかもしれませんが修正しましたので、ひきつづきナンプレ京をよろしくお願いします。

[2435]匿名希望 (2026-02-17 11:43:43)
iPhoneユーザです。
[閉じる]ボタンが見当たらない全画面広告がPLAY中にも表示されるようになりました。
何度もリロードしたり、しばらく時間を置いたり、色々対策していますが、なんとかならないものでしょうか。

[2422]らくたろう (2025-11-22 21:50:45)
Chrome、FIRST TAKEをバックナンバーからプレイ
→ クリア後、名前登録せずに「問題選択に戻る」をクリックしたところ
20万年後にタイムリープしました・・・(ちなみに人類は滅亡してました)

[2416]管理人 (2025-11-19 17:26:57)
> みんみんさま
ご連絡ありがとうございます。
メールでのお問い合わせも来たのでご案内してみます。

[2415]みんみん (2025-11-19 17:24:17)
管理人様
自己解決しました。
一旦ログオフし、ログインし直したところ、正常に動作し始めました。
マイページログイン状態でブラウザを立ち上げた場合、先程のチェック項目はブラウザ側は認識できていないのでは?と感じます。
Microsoft製品のバグはこういったものが多いように感じています。

[2414]みんみん (2025-11-19 17:11:40)
管理人様
自動保存以外はチェックが入っています。
また、メモ数字のハイライトも利かなくなっていることに気づきました。


[2413]管理人 (2025-11-19 16:47:57)
> みんみんさん
画像のように候補もコピーにチェックが入っているかご確認お願いいたします。同様のお問い合わせメールも来ましたがWindows Updateでチェックが外れたりするのかな・・・
ナンプレ画面なのですが2種類あってこのボタンで古いモードか新しいモードかが変わります。新しいモードだけにしたかったんですが古いモードが好きな方もいらっしゃって2種類存在する状況です。

[2412]みんみん (2025-11-19 16:44:04)
長押しでのコピーが効かなくなってます。
ブラウザによる現象かもしれませんが、Windows Updateの再起動後からの現象のように思います。 ちなみにブラウザは Microsoft Edge ですが、 Chrome では問題ないようです。 ダブルクリックでの入力はできています。

[2405]京子 (2025-10-28 08:04:21)
玉川中さん お久しぶりです。
お名前見つけて 凄く嬉しかったです。

[2404]管理人 (2025-10-06 09:02:33)
☆nme☆さま
無事入れてよかったです。Cookieは大きくなりすぎるとエラーになることがあるんですが、そんなにCookie使わないようにしているつもりなんですがまた確認しておきます。

[2403]☆nme☆ (2025-10-05 03:03:08)
管理人さま
ごめんなさい????
cookie消去で解決しました。
なぜ脳トレだけがダメだったのか…。遊び過ぎかな。いつも楽しませてもらってます。ありがとうございます。

[2402]管理人 (2025-10-04 19:55:26)
☆nme☆さま
ご連絡ありがとうございます。私の方からは脳トレ京に入れます。なんででしょう???
キャプチャが切れてますのでメールいただければチェックいたします。よろしくお願いします。

[2401]☆nme☆ (2025-10-04 18:14:44)
3日ほど前から『脳トレ』に入れません(泣)

[2388]管理人 (2025-07-12 14:46:03)
The First Takeの左側に広告が出ていたのでそれをSTOPしました。大変失礼致しました。
> みっひーさん
私の方では特にそのような症状は出ないようですが
キャプチャをアップしていただければ何かわかるかもしれません。
(広告ブロッカーとか通信環境のせいでしょうか????)

[2387]みっひー (2025-07-08 10:37:42)
プレイしている途中ですぐに「読み込めません」の画面に変わってしまい、また1からやり直すことになるし、firsttakeに至っては当然出来なくなってしまいます。
広告が表示されるタイミングで消える事が多いようなので、広告の種類かもしれませんが対処方法ありませんか?

[2386]TINY24 (2025-06-21 02:53:42)
> 管理人様
同じ条件で試してみました。問題ありません。
ありがとうございました。

[2385]管理人 (2025-06-20 17:06:57)
TINY24さん
本日バックナンバーを更新いたしました。これで問題なくなるはず・・・ですがいかがでしょう。

[2375]管理人 (2025-05-19 13:22:57)
TINY24さん
ご連絡ありがとうございます。現象を確認いたしました。
修正は作ったのですがアップするとFIRST TAKEを中断されている方の
データが開けなくなるので段階的なアップデートとなります。
長く中断している方のことを考えて6/19ごろにアップ予定でいきますね。
すいませんいましばらくお待ちください。

[2369]TINY24 (2025-05-14 01:12:08)
FIRST TAKE バックナンバーからレベル7の問題を選択しました。
中断しました。問題選択画面には「中断中」と表示されます。
その状態で、毎日ナンプレバックナンバーを開きました。
なぜか、こちらのレベル7も「中断中」と表示されました。

[2323]管理人 (2025-02-26 13:19:49)
> 818181818181さん
すいません。対策してみました。
今日明日ぐらいで反映されると思いますが続くようならまたご連絡ください。

[2322] 818181818181 (2025-02-24 18:06:06)
次の一手うまく表示できません。
ナンプレ本の宣伝が入り一行だけ縦長になってしまいます。
私だけでしょうか?

[2291]管理人 (2025-01-05 19:28:05)
> ナンプレ 眺めて解こう . さま
問題の作り方を間違えていました。
明日の分から2ヶ月分くらいアップしました。
すみません。23と24も同じでしたね。大変失礼いたしました。

[2290]管理人 (2025-01-05 19:06:52)
> ナンプレ 眺めて解こう . さま
ご連絡ありがとうございます。
確認いたしました。間違いなく問題は作ったのですが
アップを間違えたのかもしれません。しばらくお待ちください。

[2289]ナンプレ 眺めて解こう . (2025-01-05 18:00:43)
[2286]管理人 様
すみません。書き忘れましたが、次の一手ナンプレ の問題です。
よろしくお願いします。

[2286]管理人 (2025-01-05 13:40:20)
> ナンプレ 眺めて解こう . さま
ご連絡ありがとうございます。毎日ナンプレのレベル0と8を2024年と2023年で比べてみましたがちゃんと違う問題でした。なにか違うところが私の勘違いでしょうか?

[2283]ナンプレ 眺めて解こう . (2025-01-04 22:50:31)
管理人様
バグかどうかわからないのですが、
これまでのところ 2025年の問題は2024年の問題と同じに見えます
(もしかしたら 2024年と2023年の問題も?)。
ご確認ください。

[2200]管理人 (2024-11-19 16:27:18)
> ナンプレ 眺めて解こう .さま
すみません。この問題難しすぎてプログラムで解いている時に時間切れになったっぽいです。
回答データが入っていませんでした・・・。
回答データを入れたのでソル君は「おかしいです」とは言わなくなっていますが途中経過やヒントは入れられなかったのでご容赦ください。。。
(問題自体は複数解ではないちゃんとした難問です)

[2190]ナンプレ 眺めて解こう . (2024-11-18 00:51:28)
管理人様
この投稿 で解こうとしている問題 Lv.8 2021-04-14 ですが、
ソル君の表示が何かおかしいので 確認していただけると有難いです。

[2115]tonbee (2024-10-30 15:06:23)
管理人様
最近 頻繁に掲示板を利用させていただいています。
感謝です。
それで その投稿時の事なのですが、ほぼ毎回 1回目は「エラーです」と なります。
その後、一旦 文章をコピーしてから 色々やってると なんとか成功します。
何かエラーになるのを避けるコツがありますでしょうか。
なお 投稿はアンドロイドのスマホでしています。
追記
今回は上手くいきました。
文章の長さや 書くのにかかった時間が関係するのかな?

[2046]管理人 (2024-10-16 14:28:16)
TOPページに注意喚起を入れました。またナンプレ京のボタンには「ナンプレ京公式ボタン」と入れるようにしました。「開く」「続く」「次へ」「詳細」みたいなボタンはナンプレ京には無いはずですがややこしいなと思ったら「ナンプレ京公式ボタン」のアイコンをご確認ください。
ご指摘ありがとうございます。

[2045]管理人 (2024-10-15 19:43:27)
> hassanさん
ご迷惑おかけしています。なかなかブロックしても次から次へと湧いてくるので追いつかないんです。このあたりはGoogleが対応して欲しいところです。
みなさんも「このPCはウイルスに感染しています」が出ても
それは広告や画像なので操作不能になったら、あわてず再起動(電源ボタン長押しでのご対応お願いいたします。)
ナンプレ 眺めて解こう .がおっしゃるように再読み込みも効果的ですね。

[2037]ナンプレ 眺めて解こう . (2024-10-12 22:50:29)
「×」クリックではなく、ページ全体をリロードしましょう。
リロードすると広告は再表示されないので安全です。

[2036]hassan (2024-10-12 18:36:20)
また危ないサイトへ飛びました。Lv.7が終わって、広告が表示されたのを「×」をしたら「このPCはウイルスに感染しています」のような表示が出てフリーズしました。画像は撮れませんでした。ちょっと広告危険すぎます。

[1935]管理人 (2024-09-17 18:05:39)
ありがとうございます。
次の頁パターンですね。これも湧いてくるヤツです。フリーズしたように見えるのですが確かエスケープを長押しで脱出できたかとおもいます。それにしても悪質。ご心配おかけしました。びっくりしたでしょう。
こちらも頑張って対処していきます。
「misawa-sankyo」も報告しておきます

[1934]tonbee (2024-09-17 16:43:59)
私も14日に引っ掛かりパソコンがフリーズしました。
先ほど パソコンで探してみたら2回出てきました。
画像の緑色のボタンです。
解説の途中にあると 勘違いして押してしまうんですよね。

[1933]hassan (2024-09-17 14:59:59)
残した画像のURLが「misawa-sankyo」になっているので、ミサワホームか何かの広告に関係していたかも。ミサワがキーワードだと思います。

[1932]管理人 (2024-09-17 14:59:45)
ありがとうございます!「開<」パターンですね。なぜか「く」が「<」のヤツですね。
これはブロックしてもブロックしても湧いてくるんです。広告会社とGoogleに報告しておきます。ご心配おかけしました。

[1931]hassan (2024-09-17 14:49:26)
よく覚えておりませんが、たぶん「開く」or「ひらく」というボタンだったように思います。

[1930]管理人 (2024-09-17 13:32:22)
ありがとうございます。めっちゃ悪質ですね。
ブロックできる[次へ]ボタンだけの広告とかはブロックしているのですが、これはどんなボタンだったかわかればご連絡ください。ブロックしておきます。

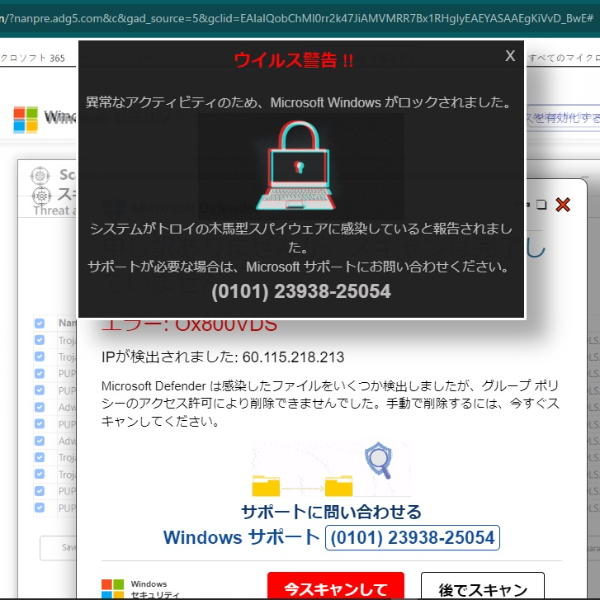
[1929]hassan (2024-09-17 13:24:08)
いつもは広告を開かないのですが、今日(9/17)誤って開いてしまったところ「ウイルス警告」といった添付画像が表示されました。たぶん悪質なスパムだと思います。広告事業者様へご注意願いたく、よろしくお願いいたします。

[1927]ナンプレ 眺めて解こう . (2024-09-16 21:49:51)
次の一手ナンプレが画像のように表示されます(android chrome です)。
治るようなら治していただけると有り難いです。

[1761]管理人 (2024-07-29 13:19:33)
> tonbeeさま
ありがとうございます。
他にもいくつか見つけました。レベル1-3までいくつか重複解が出てきます。
問題を修正してアップデートしようと思ったのですが
アプリのビルドでエラーがいっぱい出てきて困り果てているところです。
しばらくアップデートしていないうちにいろいろ変わってしまったようです。

[1758]tonbee (2024-07-26 18:26:24)
管理人さま
レベル3の問5も複数解問題でした。多分 問4と同じ原因によるものだと思いますが 念のためお知らせします。

[1755]管理人 (2024-07-26 11:49:02)
aynさま
ご連絡ありがとうございます。推移時の広告を出なくしました。まだおかしければご連絡ください。
tonbeeさま
ありがとうございます。次回アップデートで修正いたします。
重複解にはかなり気を使っているのですがたまに出てしまって申し訳ないです。

[1747]tonbee (2024-07-24 16:35:28)
管理人さま
ナンプレ京アプリのレベル3の問4が複数解問題でした。

[1723]ayn (2024-07-16 00:19:31)
FIRST TAKEで起こる事象です。
クリア後に出てくる広告を閉じると、たまにタイム登録画面に移行せず「1stチャレンジのみ受け付けます」といったポップアップが表示され、タイムが登録できないことがあります。
パソコンのGoogle Chromeでプレイしています。

[1703]管理人 (2024-07-10 10:59:12)
TINY24さま
tonbeeさま
ありがとうございます。一旦タイプ3bは取り下げます。
ナンプレラボのソルバーは簡単なテクニックはSudokuwikiどおりに解いてくれるのですがチェーン系が入りだすと多くの問題を解いてしまうので開発もかなり難儀しました。
優先順位はほぼ解説の順番通り(ベーシック・アドバンスド・エキスパート・エクストリーム)だったと思いますが最後の方のチェーン系はなんでも解いてしまったりするので多少調整したと思います。
URなどは直前の特定の状態を作り出してからURだけで解かせたりしてテストしました。ですので検出しないで他の方法で解いたりはするかと思います。

[1699]TINY24 (2024-07-09 17:08:00)
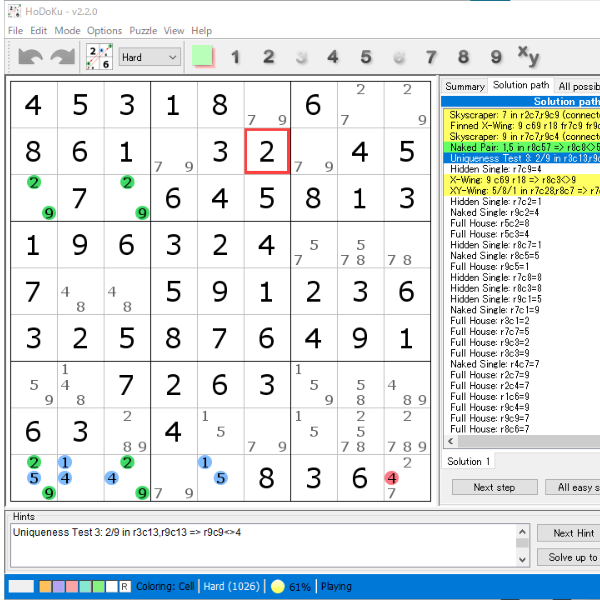
> tonbee 様
優先順位の影響は考えられますね。
余談になりますが、この HoDoKu は、私好みの設定になっています。
・Locked Candidates
・Skyscraper
・Finned X-Wing
これらの優先順位が高く設定されています。
URはナンプレのルールから導き出したものではないので
一般的には優先順位が低いのかも知れません。
URと隠れURなら前者のほうが優先順位が高そうです。
> 管理人様
実際にはソルバーとしては問題はありません。
UR3が検出されなくても、他の解法で解けています。
URを邪道と見る開発者なら、URそのものを搭載しないでしょう。
管理人さんにご負担をかけたのなら申し訳ありません。

[1697]tonbee (2024-07-09 13:46:04)
TINY24さん、 タイプ3 トリプルを使う問題を作らせるなんてすごいですね。
私も同じ問題をナンプレラボ に解かせて確認してみました。
タイプ3 トリプルは使わずに ヒドゥンURなどを使って解いていますね。
ただ、私 愛用のアプリでも解かせてみましたが、そちらでは URは一切使わずに ウイング系だけで解いていました。 アプリ推奨のヒントの採用を4回連続で拒否したところ、5回目で UR タイプ3 トリプル のヒントが出てきました。 愛用のアプリでは URの優先順位は 少し低く設定されています。(URの胡散臭さのせいだと思います)
ですので ナンプレラボが タイプ3トリプルを使わずに解いたというのは 単に プログラムで設定されている優先順位が低いからかもしれませんね。

[1696]tonbee (2024-07-09 13:04:54)
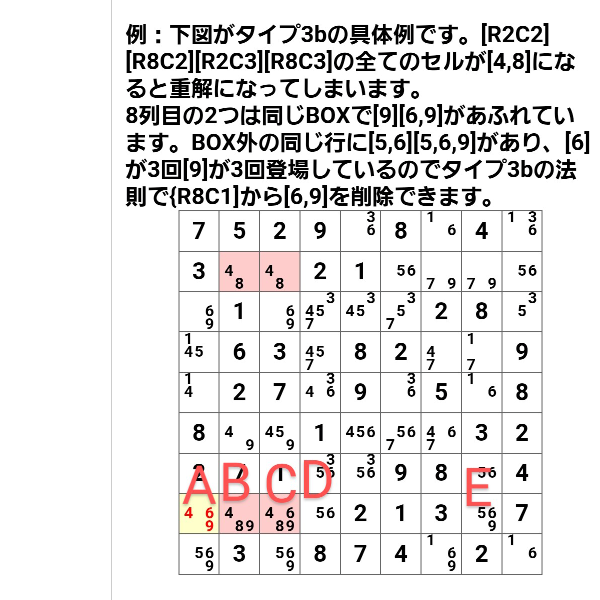
[1671] でも触れましたが 、3 b という名称についても考慮していただきたいです。
管理人さんが参考にしたと思われるSudoku Wiki では URのタイプ3 に関して、[タイプ3] [タイプ3 b] [タイプ3/3b のトリプル] の3項目にしています。
そこの[タイプ3b]で解説されているものは こちらの タイプ3bで 説明しているものとは明らかに異なります。
また こちらの 3bで使用されている図は Wiki の方では [タイプ3/3b のトリプル] のところで使われています。

[1695]TINY24 (2024-07-08 22:54:20)
テクニックのページ、ネイキッドペア・トリプルの説明を見ると
・トリプルの場合は[12][23][13]など数字が欠けていてもOKです。
とあります。
3回登場という表現を使うと、誤解をまねく可能性があります。
ナンプレラボでは、UR3で3回チェックしているのでしょうか。
画像は HoDoKu を使って問題作成させてみたものです。
r9c2(14), r9c5(15), r9c13(45)
1も4も5も2回しか登場しませんが、3国同盟です。
この問題をナンプレラボに解かせると、UR3は検出しませんでした。

[1694]管理人 (2024-07-08 15:02:29)
TINY24さん
tonbeeさん
修正してみました。もっと上手に説明できればいいのですが
ひとまずこんな感じなのかな。
https://nanpre.adg5.com/tec19_labo.html

[1672]管理人 (2024-07-04 06:31:33)
TINY24さん
tonbeeさん
ありがとうございます。
ではまた修正していきますね。

[1671]tonbee (2024-07-03 22:24:30)
TINY24さんの意見に賛成です。
私は 高度な テクニックを使うことは ほとんどありませんが、テクニックの解説を読むこと自体は とても面白く感じるので 時々勉強しています。 UR タイプ3の解説は ここでのやり取りの後 いろんなサイトで読んで ほぼ完全に理解できました。 その結果、タイプ3は かなり面白い というか とても秀逸なテクニックだと思いました。 まず 2つのマスを 1つのマスと考えて その上で二国同盟を適用する という発想が素晴らしい。 次に それを三国同盟以上のケースにも適用したというのが素晴らしい。
この素晴らしさを他の人にも味わっていただきたいので 管理人さんには 是非 そのような解説をお願いしたいです。
なお sudokuwiki.org で使われている 3b という名称(分類)は、同盟となるマスが 同じ行だけでなく、同時に 同じ箱にも存在する というパターン に対して付けられたものだと思います。 このパターンは個人的には それほど面白いとは思いませんので ナンプレ京に3bの解説がなくても気にしません。

[1667]TINY24 (2024-07-03 10:05:12)
ナンプレ京らしい文章にするのは、管理人さんのお好みですが
やはり3国同盟と関連させて説明するのが適していると思います。
ナンプレ京はおそらく sudokuwiki.org を参考にされていまが
元の図が微妙に間違っているので、ナンプレ京も影響を受けています。
https://www.sudokuwiki.org/Unique_Rectangles
H23をひとつのマスと見て69の候補があります。
48を含まないことを説明するのに、9と69が囲ってあります。
H4は6を囲っていますが、56を囲うべきです。
H8は69を囲っていますが、569を囲うべきです。
このほうが3国同盟と気づきやすいと思います。

[1666]管理人 (2024-07-03 08:59:21)
すいません。ユニークレクタングルのタイプ3bですが
修正するとしたらどのように修正するのが妥当だと思われますか?
それとも削除してしまった方がいいのかな?

[1622]管理人 (2024-06-19 10:17:27)
> ナンプレ 眺めて解こう .さん
いつも投稿ありがとうございます。とても参考になります。
編集の件ですがこちらではできますね。3時間制限にかかったとか?
修正する分がありますでしょうか?
編集テストです。編集前です。
こちらは編集後です。

[1621]ナンプレ 眺めて解こう . (2024-06-18 23:38:08)
管理人さん
投稿の編集ができません。確認をお願いします。

[1585]TINY24 (2024-06-10 03:25:06)
ある解法が本当に成り立っているかを証明するために、
細かく分けて調べるのはいいことだと思います。
その解法が使えると分かれば、もうそのことは考えません。
グループ化して見るというのは、説明不足ではありますが、
思考の過程を省略できるので全体像が見やすくなります。
B(48), C(48) は唯一解でなくなるので、これを避けます。
BCどちらかに48以外が入ればいいので
BC(69)と見ることができます。

[1584]tonbee (2024-06-09 10:39:22)
TINY24さん、 コメントありがとうございます。
私の説明は少し不足がありました。
2つの場合に分けて どっちにしても A に69は入らない としましたが、もう1つの場合について書いていませんでした。
B が9、同時に C が6になる場合です。
しかし これは B(9) C(6) D(56) E(569) となり、4つのマスに対して 3種の数字しか 入れないことになり マスが余ってしまいますので ありえません。
これも言っておかないと 不十分ですよね。
TINY24さんの言われる B C を1マスと見る というのは これを前提としているんですよね。

[1583]TINY24 (2024-06-09 00:34:23)
3国同盟の応用と考えて間違いなさそうです。
BC(69), D(56), E(569)
この形のURは、BCをグループ化して1つのマスと見ます。
URの性質から48が除外され、BC(69)と見ることができます。
3国同盟は、各数字が3回ずつ必要とは限りません。

[1582]tonbee (2024-06-08 17:06:17)
管理人さん、 Y ウイングへの対応ありがとうございます。TINY24さんも コメントありがとうございます。
今度は ユニーク レクタングルの説明 についての質問です。
実は 2月に 管理人さんに直に 質問したのですが、その後 放置していました。ごめんなさい。
その説明のある場所は 「使い方·解き方」->「 ナンプレのテクニック」->「エキスパート テクニック」->「ユニーク レクタングル」->「 タイプ3 b」 です。
この例の場合、69が3回ずつ出ると なぜ A の69が消せるのか理解できず 他のサイトなどで 調べてみました。 そして 納得できる説明を見つけました。 それは 三国同盟の理屈を使ったものです。
この例では B に9が入るか C に6か9が入るか、どちらかでないと重解になりますので どちらかが成立します。 B に 9 が入る場合、 (B 9)(D 56)(E 569) なので 569の3国同盟となり A に69 は 入れません。 Cに6か9が入る場合、 (C 69)(D 56)(E 569) の3国同盟となり やはり A に69 は入れません。 どっちになっても A に69 は入れない となります。 以上の理屈は 左下のボックスで考えても同様の結果となります。
なお この理屈だと 仮に E に 6 がなくて (E 59) であっても A の69を消せます。 なので 6 9が3回ずつ必要だという理由も分かりません。
どうでしょうか。

[1581]管理人 (2024-06-08 14:46:31)
ひとまずYウイング削除しました

[1580]管理人 (2024-06-08 10:59:16)
ほんとですね。すいません。
修正しておきます。

[1579]TINY24 (2024-06-08 02:44:06)
確かにおかしいですね。
27が翼の中心、17と12が翼の両端。
両端の1から共通して見える1を消します。
これはご承知の通りだと思います。
Yウィングだけに注目してみると、
箱2のどちらも7でない可能性があるので、他の7は消せません。
おかしい点は、3マスにそれぞれ127が入るという誤解です。
121の可能性もあります。

[1578]tonbee (2024-06-07 11:21:32)
管理人さん、お疲れ様です。
ナンプレ京、いろいろと楽しませて いただいています。
今回はYウイングについての質問です。
私の実力は Xウイングなら分かるというレベルで、Yウイングは「次の一手は Y ウイングです」と教えてもらえれば なんとか見つけられる程度です。
そんなレベルなので自信はないのですが 「入門用 : ナンプレの解き方のコツ 5」のYウイングの説明が間違っているように思います。
1と7を消していますが Yウイングでは7は消せないと思います。
どうでしょうか。

[1531]管理人 (2024-05-01 10:50:36)
> G13さん
THE FIRST TAKEの問題を間違えて毎日ナンプレにアップしてしまっていました。
明日の分から修正しました。大変失礼いたしました。

[1529]管理人 (2024-05-01 10:33:32)
> ナンプレ 眺めて解こう .さま
ご報告ありがとうございます。修正いたしました。
また何かございましたらご連絡ください。

[1528]G13 (2024-04-30 17:44:55)
相変わらずジグソー狂ですが「気まぐれ」にナンプレもします。本日のレベル8のようにレベル5や6より簡単にアッという間に解けるケースがたまにあるのは?バグというよりAIの「気まぐれ」??


[1527]ナンプレ 眺めて解こう . (2024-04-29 21:57:25)
投稿時もしくは投稿編集時に警告が表示されます。
画像アップロード時にも別の警告が表示されることがあります。
今のところ投稿自体には支障はないようです。

[1522]ナンプレ 眺めて解こう . (2024-04-26 10:52:31)
> 閉じるボタンのない広告
広告が何かの理由で拡大表示され、ボタンが画面外にはみだして、一見表示されないように見える場合もあります。
多くの場合 リロードすれば問題ないようです。
半年近く広告表示に悩まされましたが、ずいぶんと慣れてきて、もう今ではほとんど気にならなくなりました。

[1514]管理人 (2024-04-22 09:22:44)
> ナンプレ 眺めて解こう . さま
いちおうエラーは出さないようにしました。
こちらは私のプログラムのエラーが表示されている状態です。
でも表示されないだけで解決はしていないんです。
ログインできていないとかになると思うのですが、
ログインが出ないとか、まだエラーが出るようならご連絡ください。
よろしくお願いいたします。

[1513]管理人 (2024-04-21 16:29:52)
これはYahooのエラーかな。。、Yahooのログインですね。この前解決したはずなのに。また調べますね


[1512]ナンプレ 眺めて解こう . (2024-04-21 15:08:12)
> 閉じるボタンのない広告
セキュリティ絡み?の警告が表示されます。動作には支障ありません。
しかし これが広告とぶつかるとき ボタンが表示されない気がします。
気のせいかもしれませんが・・

[1509]ナンプレ 眺めて解こう . (2024-04-19 23:33:35)
管理人様
リンク復帰しました。ありがとうございます。
ボタンのない広告ですが、セキュリティ対策の絡みで表示が途中で止まって起きているようです。もう少し状況をみます。

[1508]管理人 (2024-04-19 11:34:24)
> ナンプレ 眺めて解こう .さま
投稿が増えてページがかわってしまうんですね。
ページの上限を100から1000に変更しましたのでリンクは復帰したと思います。(ただ1000以上行くとまたページが変わるので、ある程度増えてきたらスレッドを新たに作っていただければと思います。)
> あと、閉じるボタンのない広告がときどき表示されます。確認を希望します。
こちら確認したいのですがめぐり合うかどうかが難しく、キャプチャをいただければ対策できますのでぜひキャプチャをお願いいたします。

[1507]ナンプレ 眺めて解こう . (2024-04-19 10:39:07)
管理人様
1506のバグは直るか直らないかだけでも教えていただけませんか。
あと、閉じるボタンのない広告がときどき表示されます。確認を希望します。

[1506]ナンプレ 眺めて解こう . (2024-04-15 00:43:41)
管理人様
コメントへの直リンクが直リンクになっていないようです。たとえば
https://nanpre.adg5.com/bbs.php?c=19#b1156 は
https://nanpre.adg5.com/bbs.php?c=19&p=2#b1156 としないと
うまく表示されません。

[1484]管理人 (2024-02-05 17:03:58)
ナンプレ25 LV3の問題88-100の問題が同じではないかとのご指摘をいただきました。
おっしゃるとおり同じでしたので
問題83,88-100を差し替えました。
ぜひお楽しみください。

[1483]管理人 (2024-02-05 17:03:05)
TINY24さん
ご指摘ありがとうございます。
おっしゃるとおりですね。修正できると思いますのでやってみます。

[1482]TINY24 (2024-02-05 10:42:13)
いつもお世話になっています。
今回報告するのは厳密にはバグではなく仕様だと思いまが、もし改善できたら操作性の向上が見込めるので提案します。
現在の数字が1とします。
ダブルクリック入力は、現在のマウスホバー位置に1を書き込みます。このとき、誤ってとなりのマスをダブルクリックしてしまった場合、書込可能なマスなら1が書き込まれます。これは操作ミスをしたことが分かりやすく、問題ありません。
書込み不可能なマスの場合、例えば初期配置で2が入ってるマスなら、現在の数字が2に変更されて赤枠の位置に2が書き込まれます。ダブルクリックはホバー位置に数字が入ることを期待しているので、操作ミスとは気づくものの、突然違うマスに違う数字が上書きされたと感じます。
書込み不可能なマスでは
・シングルクリック 数字の変更(ハイライト)
・ダブルクリック 操作ミスと判断して何もしない
可能でしょうか。

[1358]するめ (2023-07-30 18:29:45)
TINY24さん、管理人さん
地味に気になっていた挙動が解消され、快適になりました。ありがとうございました。

[1355]管理人 (2023-07-27 10:14:50)
> TINY24さん
被ってしまった投稿を消しておきました。

[1354]TINY24 (2023-07-26 22:10:50)
すみません、掲示板を汚してしました。
なんで3回も??

[1351]TINY24 (2023-07-26 20:01:33)
> 管理人さん
長時間テストプレイしたので、たぶん大丈夫だと思います。
ありがとうございました。
別件で気になるところがありましたが、気のせいかもなので、
もう少し調べてみます。

[1350]管理人 (2023-07-26 16:19:26)
> TINY24さん
修正してアップしました。どんな感じでしょう?お試しください。

[1349]管理人 (2023-07-24 17:47:37)
> TINY24さん
確認いたしました。おっしゃる通りですね。
対応できると思いますのでしばらくお待ちください。

[1348]TINY24 (2023-07-24 17:05:45)
いつもお世話になっています。
現在の仕様では、マスのハイライトが変化するタイミングは、
・数字ボタンを使ったとき
・パズル上の確定数字をクリックして、注目している数字を変えたとき
ですが、以下の例ではハイライトが変化しせん。
あるマスを数字1に確定させるために、数字1のボタンを押します。
数字ボタンを使ったので、そのマスは黄色の背景色になります。
それは勘違いで、まだ1は確定していなかったという場合があります。
このマスをメモ数字1にするために、メモ数字1のボタンを押します。
このとき、マスの背景色が変化しません。
処理としては、メモ数字1の部分を黄色にしたと思われますが、
マス全体が黄色になっているので、変化が分かりません。
実際には、確定数字1をキャンセルしてメモ数字1にしたので、
いったんそのマスのハイライトを消す処理が必要かと思われます。
一手戻るボタンを使って、確定数字のマスがキャンセルされた場合も、
同様の現象になります。
説明が下手で申し訳ありませんが、伝わりましたでしょうか?

[1306]管理人 (2023-06-07 16:32:30)
> Jupiterさん
1日一回だけですのでその日初めての場合は弾かれないようになっております。
毎回弾かれますでしょうか?

[1303]Jupiter (2023-06-06 10:53:44)
THE FIRST TAKE
その日初めて開いても弾かれるのはなぜですか
ちなみに今日は6と8で弾かれました

[1255]みんみん (2023-04-10 11:53:49)
>管理人様
すみません、間違えてました。
「バックアップ」ではなく「バックナンバー」でした。
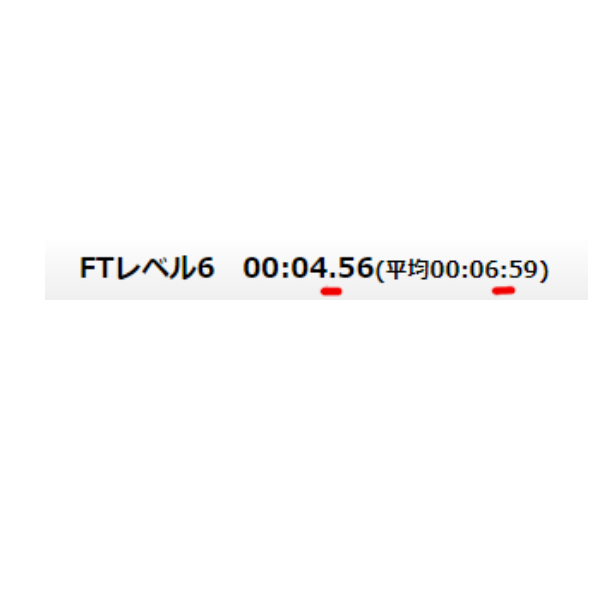
それとは全く関係ない(多分ミスタイプ)ですが、タイム表示がプレイヤータイムの表示が「**:(コロン)**.(ピリオド)**」となっています。平均タイムの方は「**:**:**」と両方とも「:(コロン)」になっています。

[1254]管理人 (2023-04-10 09:51:57)
> みんみんさん
すいません。確認いたします。

[1253]管理人 (2023-04-10 09:51:40)
>ナンプレ 眺めて解こう .さま
修正いたしました。ちゃんと原因究明ぜずになおしてしまったので
またおかしくなったらご連絡ください。

[1252]みんみん (2023-04-09 20:18:20)
管理人様、「THE FIRST TAKE バックアップ」について、
別の端末からのアクセスでは、それまでクリアしたデータのタイムが表示されません(「毎日ナンプレ」ではちゃんと表示されました)。 当日分は以前に指摘したことがありましたが、今回はバックアップ分のデータが別端末に継承されない症状です。 出先で暇つぶしにやろうとした際に気づきました。

[1251]ナンプレ 眺めて解こう . (2023-04-09 11:17:33)
管理人さま すみません。
投稿で何かミスして おかしなことになってしまいました。
https://nanpre.adg5.com/bbs.php?c=25#b1245
修正(削除?)をおねがいいたします。

[1239]管理人 (2023-04-03 17:10:02)
ナンプレ 眺めて解こう .さま
バックナンバー修正しました。
選択されている月の最終日まで表示されるようにしているつもりだったのですが今月の30日までになっていました。

[1238]管理人 (2023-04-02 11:16:59)
ナンプレ 眺めて解こう .さま
ご連絡ありがとうございます。失礼いたしました。
月曜日になおしますね。

[1237]ナンプレ 眺めて解こう . (2023-04-02 11:09:48)
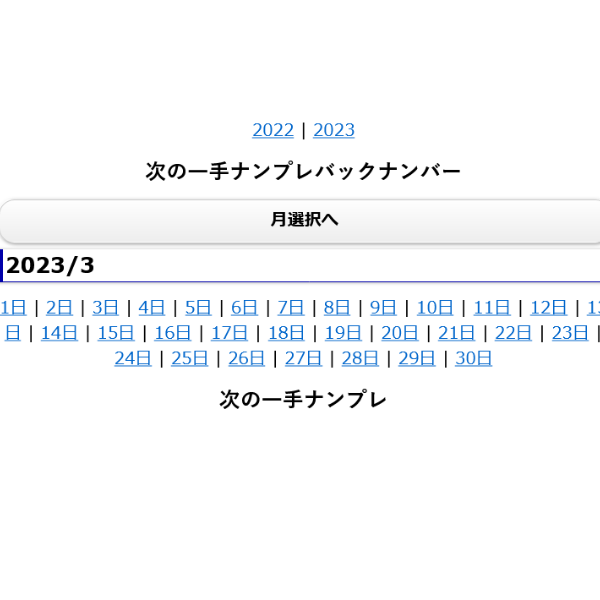
次の1手のバックナンバーの月選択は どの月も 1~30日になっています。

[1235]ナンプレ 眺めて解こう . (2023-04-01 10:23:41)
管理人様
バックナンバーに3月31日が表示されない?ようです。
もしかして エイプリルフール?


[1200]Jupiter (2023-03-15 16:14:00)
チェックのオンオフをしても変わらないので、試しにチェックを外してみたところ、コピペができるようになりました…
いずれにしてもお騒がせしました

[1197]管理人 (2023-03-14 19:28:17)
> Jupiterさん
一度チェックボックスをオン オフ オンとしてもらうとなおることがあります。
お試しください。

[1196]Jupiter (2023-03-14 19:07:41)
ありがとうございます
が、残念ながらチェックされているのを確認しました
現在も同様に問題の種類を変えてもコピペできません…
候補の数字を書かずにチャレンジしてみます

[1195]管理人 (2023-03-14 16:01:36)
> Jupiterさん
長押しのコピペでしょうか?
毎日ナンプレの問題を選ぶところで「候補もコピー」のチェックが入っているか確認してもらえますでしょうか?
https://nanpre.adg5.com/index.php#01

[1194]Jupiter (2023-03-14 15:11:17)
昨日の夕方頃からコピペができません
気のせい?

[1186]管理人 (2023-03-13 14:42:48)
> もっさnさま
Lv.8はナンプレラボの出張問題ですので、ものすごく簡単なな問題がくることもあります。それも含めて楽しんでいただければと思っているのですがひょうしぬけでしょうか。
頻度がおおくなってしまったのかもしれません。

[1184]もっさn (2023-03-13 03:21:46)
最近、たまにFIRST TAKE LV8が異常に簡単なのは仕様でしょうか?

[1160]管理人 (2023-03-01 16:53:47)
> ナンプレ 眺めて解こう .さま
ご連絡ありがとうございます。修正いたしました。
Yとyは違うのですが、どちらでも行けるようにしました。
また未来の場合は問題が出ないようにしました。


[1154]ナンプレ 眺めて解こう . (2023-03-01 11:23:00)
https://nanpre.adg5.com/back_number_itte.php?Y=22&m=6&d=17
上のURLを入れると 未来の問題? が表示されます・・・???
?Y か ?y で違うようです。
https://nanpre.adg5.com/back_number_itte.php?y=22&m=6&d=17

[1151]じん (2023-02-28 00:00:56)
広告画面から先に進みません
何回も繰り返し広告が出る

[1139]するめ (2023-02-24 06:45:28)
管理人さん
ISO 8601 では、ミリ秒まで表す場合は
hh:mm:ss.sss (拡張形式)
だそうです。時分秒はそれぞれコロンで区切るのが一般的かと思います。

[1136]管理人 (2023-02-22 15:16:34)
00:00.00の表記はどこかで調べたような気がしますがどこだったかな。気のせいですかね。00:00:00のほうがわかりやすいですかね。

[1135]管理人 (2023-02-22 15:08:58)
> hassanさん
2回登録の件、お問合せフォームより送信していただければ
対策いたします。すいませんがよろしくお願いいたします。
https://nanpre.adg5.com/mail_contact.php


[1134]hassan (2023-02-21 14:24:47)
>[1131]するめ さんへ
確かに名前の頭に数字を使っている人がいるときは、何か分かりづらいですね。
時間と名前の間は [:](コロン)ではなく、[_](アンダーバー)もしくは[/](スラッシュ)の方が分かりやすいのではないかと思います。


[1133]hassan (2023-02-21 08:58:36)
きょう(2/21)も出来ました。

[1132]hassan (2023-02-20 17:48:29)
きょう(2/20)FT 3問とも2回出来ました。(同じアカウントなのに)
TIME が同じ程度なので、近い順位で見つかると思います。
詳細をココに書いてしまうと、マネする人が出てまたタイム荒らしになっては困るので、管理人様へは別途何らかの方法でお伝えしようと思います。

[1131]するめ (2023-02-20 16:36:55)
管理人様
タイムを登録すると表示されるランキングが
[1]00:03.12:inu
[2]00:03.33:saru
[3]00:03.33:kiji
という形式になっています。The First Take のベストテンも同様。
これで困るというわけではないのですが、分(nn)と秒(ss)の間の区切りはドット(.)ではなくコロン(:)に統一した方がスッキリします。すみません、細かくて。
(Twitterをフォローしていただき恐縮です)

[1130]管理人 (2023-02-20 15:38:44)
> hassanさんありがとうございます。
つぎに私の方でおかしいときにログを取って送る手筈になっております。
その時に一緒に送信させていただきますね。

[1128]hassan (2023-02-20 10:11:28)
きょう(2/20)FT 30秒の広告再生のとき、10秒を過ぎたあたりで広告が消えました。「OK」ボタンを押し、プレイはできました。
先週くらいにも一度起こった現象です。
ブラウザは Chrome です。
フリーズ時のスクショを撮ったので添付します。

[1114]管理人 (2023-02-10 19:14:41)
> hassanさん
わたしも本日Safariで出ませんでした。広告会社さんにキャプチャを送ってみました。
もしChromeで出ないようでしたら、ログを送ってもらえればとの事ですがChromeで出ないようでしたらぜひお問合せフォームよりご連絡ください。

[1112]hassan (2023-02-10 08:50:45)
きょう(2/10)私も広告が表示されませんでした。
頻繁ではありませんが、過去にも稀に出ていた現象だと思います。
たぶん広告の切り替えやサーバーの更新など、アクセスするタイミングによって広告が表示されないのでは?と思います。

[1109]管理人 (2023-02-03 15:39:38)
おさぴーさん
ひとまず大丈夫でしょうか?
検証方法を広告会社さんに聞きましたので
また頻繁に広告が出ないようならお問い合わせフォームよりご連絡ください。

[1106]おさぴー (2023-02-01 21:05:28)
今日は広告出ました(⌒∇⌒)
我が家のPCのせいか、ネット環境か、知識なさ過ぎてわからないのが悲しいです。PC新しいのにして一年半経つし、スマホなら問題なく広告出ます。
同じログインしてもPCでプラウザが違う(スマホも)とタイムは残らない事に気が付いて…
コンプリート出来るだけしたいんです。
このまま広告で続けますように

[1105]管理人 (2023-02-01 14:04:08)
> おさぴーさん
ご報告ありがとうございます。
広告の運営会社さんにどういう情報があれば調べられるか聞いてみます。

[1104]管理人 (2023-02-01 14:03:01)
> みんみんさん
ご報告ありがとうございます。
プレイ画面へはTOPやバックナンバーやじっくりナンプレなど
いろいろなところから行けるのでどこから来たかを記録しているのですが
その記録がうまく行っていないようですね。
もしそうなら他にも不具合が出てくるかもしれません。
しばらく様子を見ていただければと思います。

[1103]おさぴー (2023-01-31 20:49:39)
最近THE FIRST TAKEの広告が出ない時ときが頻繁にあります。
ブロックもしていないし。どうしてなのかがわからない。
設定も変えてないし。
普段Microsoftedgeを使っていますが、Googlechromeでやっても広告出たりでなかったり。
不思議です。

[1102]みんみん (2023-01-28 15:07:27)
難問レベル6、問題35をクリアして「トップに戻る」をクリックしたら「THE FISRT TAKE」バックアップの方へ飛んでいきました。
以前、クリア画面の背景画だけ更新されトップに戻れない、という指摘を対応していただきましたが、極稀に解消されていないケースもあります。 大した問題ではありませんが気になりますのでご報告まで。

[1097]みんみん (2023-01-20 12:59:49)
今投稿して気付いたら、何の音もせず「投稿が終わりました」ってメッセージが「投稿する」ボタンの下に現れただけでした。

[1096]みんみん (2023-01-20 12:56:50)
プッシュ通知は何のための機能だろうと感じてました。
自分が投稿したときに「ポロ~ン♪」って鳴った音しか聞いたことがありません。
因みにブラウザは Chrome です。

[1095]管理人 (2023-01-20 10:43:15)
> TINY24さま
確かに自分の分しか出ない感じですね。
なんでだろう。自作したのでバグかな・・・・?
もうちょっと調べてみます。みなさんも来ていないでしょうか?

[1094]TINY24 (2023-01-20 04:55:51)
「プッシュ通知を許可する」について教えて下さい。
掲示板の更新時に、右下にポップアップ通知が出るイメージです。
今のところ、自分が投稿した瞬間しか出現しません。

[1093]TINY24 (2023-01-20 04:51:57)
> 管理人さん
お返事遅くなりました。
N国同盟の結論部分、確認できました。
ありがとうございました。

[1092]ステファン (2023-01-17 12:28:05)
>管理人さん
ありがとうございました。出来る様になりました。

[1091]管理人 (2023-01-17 11:13:11)
> ステファンさん
こんにちは。先ほど同じ問題をスマホで解きましたが大丈夫でした。
iPhoneでもAndroidでも動きましたでのステファンさんのスマホの問題がありそうです。
一度ブラウザを変えてやってもらえますでしょうか?
それでうまくいけばブラウザの問題ですのでクッキーなどがあやしいです。うまくいかない場合はネットワークセキュリティのような問題かもしれません。(会社のWiFiがブロックしてるとか)
一度ブラウザを変えてお試しいただけますでしょうか?


[1090]ステファン (2023-01-17 10:40:00)
管理人さん
最近(といっても数ヶ月前から)スタートの数字が白で数字を入れると時計が止まってしまいます。それでも数字を入れ続けるとキラキラで止まってしまい固まってしまいます。当然時間が止まっているのでタイムは記録されません。数日間プレイをやめるとまた出来る様になるのですがすぐに上記の状態に戻ります。私のスマホがおかしいのでしょうか?

[1089]するめ (2023-01-16 18:39:03)
管理人さん
ご対応ありがとうございます。これらの問題の三分の一くらいは解くことができるようになりたいものです。

[1088]管理人 (2023-01-16 17:27:08)
>するめさん
修正いたしました。
THE FIRST TAKEのが混じっていたもようです。

[1087]管理人 (2023-01-16 15:26:43)
> するめさん
なるほど!確認しました。ありがとうございます。
ここにも出ないはずなんですが・・・・
修正いたします。ありがとうございます。

[1086]するめ (2023-01-16 15:07:21)
管理人さん
私が立ち寄ったページはこれです。
https://nanpre.adg5.com/writescore_nanmon.php?lv=8
スクショを撮った問題のタブには
難問ナンプレ(無料) 2021/08/28 レベル8 問題239
と表示されています。
いろいろ情報不足、確認不足ですみません。

[1085]管理人 (2023-01-16 14:32:42)
> するめさん
こんにちは。毎日ナンプレのレベル8は2022スタートですので
2021の一覧にレベル8は出ないはずなのですが出ていますでしょうか?

[1084]するめ (2023-01-16 14:09:04)
難問ナンプレ 2021/08/28 レベル8 問題239
レベル8はリストの上から15問がこんな感じ。他のレベルは確認していません。

[1083]管理人 (2023-01-16 13:19:31)
> TINY24さん
ありがとうございます。
確認いたしました。2国同盟・3国同盟では
[=>[R?C?]から?を削除 ]
が出ていませんでした。こちらは私のプログラムミスです。
修正しましたので機会があればご確認ください。

[1078]TINY24 (2023-01-15 01:34:44)
> 管理人さん
あれからいろいろ試してみたのですが、意外と多くはありませんでした。
今のところ、2国同盟・3国同盟がそのケースです。
確か以前、簡単な解法は思考ルーチンが別だとおっしゃっていたので、
それが原因かも知れません。

[1075]管理人 (2023-01-13 16:28:17)
> TINY24さん
=>と->は意味は同じです。統一できていないだけでした。
矢印以降の文章ですが
プログラムとしては削除の方を先にしますので削除ができれば
(正確には変更があれば)
=>[R?C?]から?を削除
のような文章が削除された場合つくられます。
削除ができた場合は解説文章を組み立てます。(下記のようなの)
> (pointing_pairs)が9番目のBOXで成立。
> 5が7行にだけ存在。BOX外の7行から5を削除します。
ということで=>以降がないのに解説文章だけが出る場合はおかしいですね。ちゃんと精査できていないのですが最初からAIが解く場合と、途中まで人が解く場合では状況がだいぶ違うのでそのせいかもしれません。
(消すべき候補が無いとか)
つぎにおかしいところがあればキャプチャをとっていただければ確認できるので、お手数でなければお願いいたします。

[1071]TINY24 (2023-01-12 02:27:42)
> 管理人さん
すみません。「または」は私の言葉で、そこは重要ではありません。
使っている記号が2種類あったので、そう説明しました。
ポインティングペアの例なら、この矢印 =>
他の例なら、この矢印の場合もあります ->
重要なのは矢印以降の文章があるかどうかです。
矢印は「よって」のような意味で、その後に結論が述べられています。
結論が書かれていない場合があるのでは、と質問しました。
矢印以降の文章がないものは、
・その解法は成立したが、削除する部分がない
・その解法は成立したが、あなたはすでに削除している
・解法によっては、削除する部分の説明はない
どの理由でしょうか?

[1067]管理人 (2023-01-11 10:13:45)
> TINY24さん
プログラムを検索しましたが「または」という言葉が出てくるのは
「ユニークレクタングル タイプ3」だけですね。
ポインティングペアだと下記になると思います。
すいません疑問となるメッセージをキャプチャしてもらえると解決が早いかと思います。よろしくお願いいたします。
=====ここから=======
ポインティングペア
(pointing_pairs)が9番目のBOXで成立。
5が7行にだけ存在。BOX外の7行から5を削除します。
=>[R7C5]の候補5を削除
=>[R7C6]の候補5を削除
=====ここまで=======

[1057]TINY24 (2023-01-08 06:34:05)
1手先(5秒+) を押したときのヒントについて教えて下さい。例えば、
ポインティングペア
(pointing_pairs)が9番目のBOXで成立。
5が7行にだけ存在。BOX外の7行から5を削除します。
=>[R7C5]の候補5を削除
=>[R7C6]の候補5を削除
=> または -> 以降の文章が、ここではありますが、ない場合があります。
・その解法は成立したが、削除する部分がない
・その解法は成立したが、あなたはすでに削除している
・解法によっては、削除する部分の説明はない
どの理由でしょうか?

[1046]管理人 (2023-01-04 10:34:07)
マイページの7・8が今年に入ってから更新されません。
とのご指摘をいただき修正いたしました。
今日から明日にかけて反映されていくと思いますが
ログアウト・ログインでも反映されるはずです。よろしくおねがいいたします。
ご指摘ありがとうございました。

[1042]みんみん (2023-01-01 06:26:59)
>管理人さま
年明け早々のご対応ありがとうございます。
m(__)m
今年もどうぞよろしくお願いいたします。

[1041]管理人 (2023-01-01 00:19:39)
> みんみんさん
グループXサイクルだけっぽいですね。修正しました。

[1039]管理人 (2022-12-30 17:33:32)
あららら。
なんでしょう。。。また見ときますね。

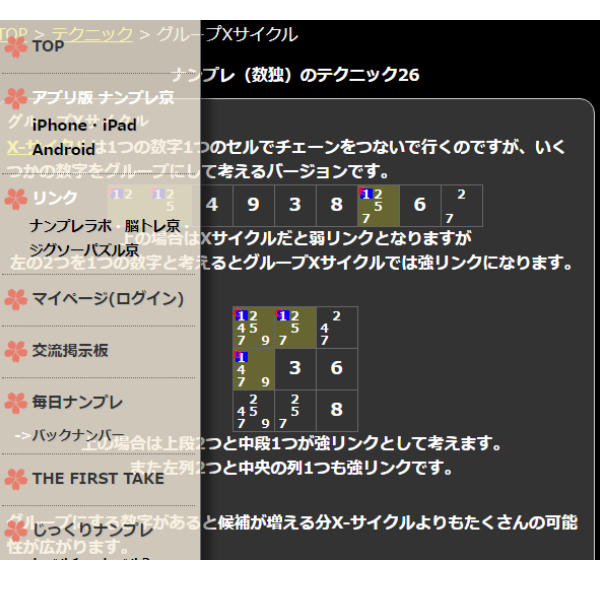
[1038]みんみん (2022-12-30 17:28:42)
>管理人さま
すいません新たな不具合を見つけてしまいました。 (^_^;)
左側のフレームメニューが解説本文に重なってしまってます。

[1037]みんみん (2022-12-30 17:23:45)
>管理人さま
ありがとうございます。 すべて確認したわけではありませんが、普通に見えるようになっていました。 エグゾセって言うのがどのようなテクニックなのかを見たかった次第です。(まだ理解できていませんが)
年末ギリギリまでお手数をおかけしました。

[1036]管理人 (2022-12-30 11:20:32)
> みんみんさま
修正したのですがいかがでしょう。

[1035]管理人 (2022-12-28 16:38:31)
> みんみんさん
ご連絡ありがとうございます。そこはできていませんでしたか。
確認いたします。
> G13さん
すいません。確認いたしました。全てのピースをランダムにしているかなかな。たしかに最初からトレーの数がおかしいですね。
> masakoさん
マイページの下の方に記録をリセットがあります。下記URLです。お願いいたします。
https://nanpre.adg5.com/mypage04.php

[1034]masako (2022-12-28 16:12:09)
管理人様
全て(もしくは部文的)の個人データのリセットはどこから行えるのでしょうか?

[1033]G13 (2022-12-27 17:27:31)
ジグソー本日の梅田スカイツリーですがトレーと残ピース数が一致してませんでした。以前もこのような事がありましたが、パズル作成には何ら支障はございません。きっと当方PCのメモリ不足か風邪でもひいたんでしょう(笑)

[1031]みんみん (2022-12-25 09:25:49)
>管理人さま
「テクニック」からの殆どの解説ページがダークモードに対応できておらず非常に見辛いです。(というか見えません)
ご対応の程よろしくお願いいたします。

[1030]管理人 (2022-12-23 12:05:05)
> みんみんさんご指摘の「最初から」を選択した場合については、まだ直っていないようです。
見落としていました。こちらも修正いたしました。
動作がおかしければご連絡ください。

[1029]TINY24 (2022-12-22 20:47:51)
> 管理人さま
クリアボタンについては期待通りになりました。ありがとうございました。
みんみんさんご指摘の「最初から」を選択した場合については、まだ直っていないようです。

[1027]管理人 (2022-12-21 15:57:42)
数字のグレイになる問題修正しました。
数字を入れる時、消した時に数字の数を数えて9つならボタンをグレーにします。10とか8になる場合はボタンの色は復帰します。
(ナンプレ・ナンプレ候補もコピー画面・ナンプレ6・ナンプレ16旧画面)
「ダブルタップで数字を置く」の表示がONなのにダブルタップにならない場合があるのを修正しました。

[1019]管理人 (2022-12-19 09:53:49)
> みんみんさま
ありがとうございます。
PCに保存されている状態がリセットされると「ON」になるようになっています。リセット状態ではチェックボックスも「ON」にするようにプログラムしているのですが、なんでかな・・・。前にもそんなことがあったような気がします。ちょっと見直してみますね。

[1018]みんみん (2022-12-17 17:04:03)
>管理人さま
結論:チェックのオン・オフが有効になりました。
・従来どおり「オフ」の状態でダブルクリックが有効を確認
→チェック「オン」でもダブルクリック有効を確認
→チェック「オフ」でダブルクリック「無」効を確認
→チェック「オン」でダブルクリック有効
ただ、このチェックボックスに気付いたときに「オン・オフ」を試してみてどちらでもダブルクリックが有効だったので「オフ」のままにしていた、という状況でした。

[1017]管理人 (2022-12-17 16:23:25)
> みんみんさん
> 因みに、「ダブルタップで数字を置く」のチェックは外したままですがPCの「ダブルクリック」で入力できます。
ほんとですか?私の方ではなりませんねぇ。チェックのON・OFFをしてから再度試していただけますか?

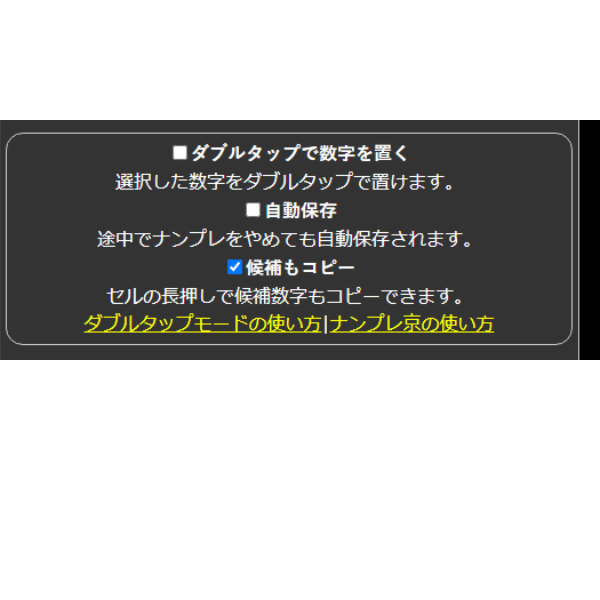
[1016]みんみん (2022-12-17 11:49:52)
因みに、「ダブルタップで数字を置く」のチェックは外したままですがPCの「ダブルクリック」で入力できます。 タブレットとでは意味が異なるのでしょうか?

[1015]みんみん (2022-12-17 11:42:48)
>管理人さま
> 余分に入れた場合や削除した場合にグレーを戻すのはあえて入れて
正誤は無視して、とりあえず数字が9個揃った時点で一度グレイアウトしますが、10個目の入力(ダブルクリックで入力できます)で解除されます。

[1014]管理人 (2022-12-16 15:57:52)
> TINY24さま
> みんみんさま
数字のグレイの件承知しました。いちど検証してみます。
実は全部揃った時点でグレーにするようにはしていましたが
余分に入れた場合や削除した場合にグレーを戻すのはあえて入れていませんでした。
というのも確実にグレーを表示するプログラムは何か入力するたびに毎回計算しないといけません。その分動きがもっさりしたりすると嫌だなと思ったのです。
で、そこで困るケースはあまりないかなと思い省略しました。動きがもっさりなるかどうかはプログラム方法や使っているマシンにもよりますが最近はマシンのスペックも高いので問題ないかもしれません。
いちど検証してみますね。

[1013]みんみん (2022-12-15 05:04:24)
TINY24さんの意図に関連するか分かりませんが、
ある程度埋めた後でミスに気づき「最初から」を選択すると、盤面の数字はリセットされますが、確定数字の方はリセットされずグレイアウトを維持しております。 極端な話、すべての数字がグレイアウトしていた場合、何か数字を入れた後に漸くグレイアウトが解除されます。
この症状は改善していただきたいなぁ、と思ってました。

[1012]TINY24 (2022-12-14 19:39:24)
> 管理人さま
パズル初期配置に1の数字が3個あるとします。
どこでもいいので、空いてるマスに1を入れていきます。
6個入れたら、3+6=9個となり、1のボタンはグレーになります。
さらに1を入れると10個になり、1のボタンは黒になります。
正解不正解はおいといて、ちょうど9個ならグレーになる仕組みです。
1を入れたマスの上から、2を上書きします。
1が減って再び9個になったので、またグレーになりました。
9個ならグレーというチェックは、数字ボタンを押したときに判定されます。
1が10個のときに、クリアボタンで消します。
1が減って9個になりましたが、1のボタンの色が変わりません。
クリアボタンを押したときにも9個チェックを入れようという提案です。
現状では、変なタイミングでグレーに戻るように見えます。

[1011]管理人 (2022-12-14 09:58:15)
> TINY24さま
ご提案ありがとうございます。
入れた数字(例えば1)を全部消したらクリアボタンも薄くするということでしょうか?
その場合でしたら1を全部消しても2は残っているのでクリアボタンをグレーにしたらややこしいように思いますがいかがでしょう。

[1010]TINY24 (2022-12-12 09:01:12)
数字1を入れる
→ 数字1が合計9つになったら、ボタン1をの色を消す
この処理を、クリアボタンにも適用したほうがいいと思います。
クリアボタンを押す
→ 消された数字が合計9つになったら、そのボタンの色を消す

[1006]masako (2022-11-23 19:58:47)
[1000]で候補数字の着色について聞きましたら、回答を頂きました。
ありがとうございます。
ですが、「表示候補もコピー。セルの長押しで候補数字もコピーできます。」の表題に、「候補数字もハイライト表示になります」とか書いて欲しいですね。

[1005]TINY24 (2022-11-23 08:42:59)
> みんみんさん
ハイライトなしは、パターン認識の訓練にはなったかもです。ただ、ヒントを使う場合に、1回操作しただけで消えてしまうのはあんまりだと思ってたので、毎回スクショを撮ってやってました。これがハイライトで解決したのはありがたい。

[1004]みんみん (2022-11-22 17:43:16)
>TINY24さん
この機能を使わずにやってこられたことに∑(゚◇゚ノ)ノびっくりです☆彡

[1003]TINY24 (2022-11-22 16:27:28)
候補数字のハイライトあったのか……。
知らんとやってた。

[1002]管理人 (2022-11-22 10:03:55)
> みんみんさん
ありがとうございます。
> masakoさん
ご確認ください。
なんだか年末進行っぽい感じでばたばたしております。

[1001]みんみん (2022-11-20 08:38:51)
>masakoさん
[742][743]のコメントは役に立ちませんか?

[1000]masako (2022-11-19 17:07:31)
以前は候補数字が黄色くなったのですが、4.5日前からならなくなりました。どこで設定するのか教えて下さい。

[999]管理人 (2022-11-16 18:57:00)
> するめさん
問題ないです。すでに上がっていても忘れてたりもあるので
報告いただけるとありがたいです。
(今回はナンプレ自体のバグでもないのでちょっと安心です)
ところでTOPにときどき出てくるソリティア。脳トレ京の出張問題ですが、これがときどきおかしな動作になって、なおしたくてもなかなか再現せずにどうしたもんかとなっておりますが、ソリティア自体はなかなか楽しくできているのでぜひでてきたら遊んでみてください。タイムとかないのでゆったりブレイクです。

[998]するめ (2022-11-15 21:09:32)
あ、すでに982で報告が上がっていたのですね。
スレをよく読まずにすみませんでした。

[997]管理人 (2022-11-14 14:09:02)
> するめさん
ご連絡ありがとうございます。
この件、代理店に連絡済みでして、現在Googleのほうで調査していただいているそうです。

[996]するめ (2022-11-14 11:43:24)
The First Take の広告について
広告のサイズがフレームに比べて大きすぎる、つまり、広告がトリミングされた状態で表示されることがあります(不動産ファンドの広告)。PC + Windows + Chrome です。
私だけの問題かもしれません。そちらの環境でこの問題が再現されない場合は、お手数ですが本メッセージを削除してください。

[994]管理人 (2022-11-14 11:00:50)
> みんみんさん
難問ベスト50修正しました。こちらリンクが前の画面だけになっていました。
(候補の長押しでコピーがオンかオフかで画面が違います。)
修正いたしました。しかも他のレベルが表示されていなかったので
それも修正してレベル8、難問ナンプレ、ナンプレ16のレベル6、7を付け加えました。

[989]めいくう2 (2022-11-12 16:32:51)
>管理人さん
問題83の横に表示されるものですがもう既に違う記録に上書きしました。
前の記録は直近のベスト20の中に入っていないのでどういう訳か消えているようです。

[986]管理人 (2022-11-11 17:44:19)
> hassanさん
代理店の方に伝えたら再現したとのことで
現在Googleで調べていてくれているそうです。
> みんみんさん
しばらくおまちくださいませ。

[985]hassan (2022-11-10 08:05:23)
>管理人さん
了解しました。しばらくしたらチェックして、また何かあったら連絡します。
※ ビワイチ頑張ってください。レポートや写真、楽しみに待ってます。

[983]管理人 (2022-11-09 13:09:03)
> hassanさん
私の方では正常に表示されます。
拡大表示されているとかかなとも思ったのですが、拡大表示しても大丈夫でした。いちおう代理店さんに報告しておきました。
ありがとうございます。

[982]hassan (2022-11-08 09:19:57)
管理人さん
動作の問題ではないのですが、FTで表示されるCMが最近拡大され画面内に収まっておりません(左上が固定され150%くらいになっている感じ)。スポンサー様にとっては伝えたいことが伝わらず、広告媒体としての機能を満たしておりません。スポンサー離れにならないように改善された方が良いと思います。


[981]管理人 (2022-11-07 12:06:13)
> めいくう2さん
消したわけではないのですがめいくう2さんの記録で15分台のはありませんでした。登録されたタイムの話でしょうか?
それとも問題83の横に表示される自身のタイムでしょうか?



[980]みんみん (2022-11-05 14:12:25)
いつもお世話になります。
特に致命的というわけではないのですが、「難問ベスト50」から挑戦する場合と、普通に「じっくりナンプレ」で始める場合とで固定(確定)数字を選択したとき、メモ数字の挙動として、ハイライトされない/される、という違いが有るようです。
もしお時間が有るようならご対応いただければ、と思います。

[979]めいくう2 (2022-11-05 07:36:26)
ナンプレ16 レベル6 問題83について要望があります。
僕の記録がとんでもなく早い記録になっています。
僕はいくら何でも15分台でこの手の問題を解けた試しがありません。
実際1時間近くかかっていたと思います。
恐らく中断した後の再開時に中断前の記録が反映されていないためだと思います。
記録の取り消しをお願い致します。
ちなみに僕は旧プレイ画面での操作です。

[978]管理人 (2022-11-01 07:05:05)
すいません。ありがとうございます。
みんみんさんよりメールもいただきました。
暗号化通信の更新をしていたのですが、有効化ボタンを押していませんでした。ご迷惑をおかけしました。
恐ろしい‥来年は気をつけます

[977]TINY24 (2022-11-01 00:05:27)
このサーバーが nanpre.adg5.com であることを確認できませんでした。セキュリティ証明書の期限が昨日で切れています。

[975]管理人 (2022-10-25 09:14:49)
> にっちやんさん
すいません。ご迷惑おかけしております。
ブラウザはクロムでしょうか?
もしかしてウイルスソフトかなぁとも思いますがブラウザを変えたりウイルスソフトを一時OFFにして試していただけますでしょうか?

[974]にっちやん (2022-10-22 13:35:09)
みんみんさん
突然すみません!
私も広告ブロックしてないのに広告が出てこず問題が解けなかったり、メモ数字・確定数字が変わってることがたまにあります????
みんみんさんだけのバグではないと思ったのでコメントさせていただきました。

[973]管理人 (2022-10-21 20:01:02)
みんみんさん
これは。問題がバグってますね。いかんいかん。楽しみにしていただいているかたすいません。


[972]みんみん (2022-10-21 19:55:04)
そういえば、今日の「次の一手ナンプレ」もどのセルに対する設問かわかりませんし、回答数字もクリックできませんが、これも私限定の現象なのでしょうか?

[971]みんみん (2022-10-21 19:51:30)
>管理人さん
今、試したところ、広告なしで挑戦できるようになっていました。 通常は広告ブロックのアドイン(uBlock origin)を無効にしないと例のメッセージが出たままになるのですが、今日対応いただいたケースでは、アドイン有効でも入れてしまいました。
これはこれで異常な気がしますので、元に戻していただいても結構です。 バックナンバーで挑戦することにしますので。 なにやら私限定の不具合が色々あるようなので申し訳ないです。
メモ数字・確定数字が気づけば変わっている件、セル入力中に強制TOPメニューに戻される件、、、なんでなんだろう??
メモリー32GBだとダメ、とかはないですよね?

[970]管理人 (2022-10-21 18:30:12)
> みんみんさん
ひとまず応急処理でみんみんさんは入れるようにしました。
治りましたら解除しますのでご連絡くださいね。
> 昨日からコメントいただいていたのに気がつかずすいません・・・
なんか別のことしていました・・・汗

[969]管理人 (2022-10-21 18:21:26)
> みんみんさん
こちらのほうでテストしたのですがMacでもWindowsでも大丈夫でした。なんででしょう・・・・


[967]みんみん (2022-10-20 12:05:33)
>管理人さん
「THE FIRST TAKE」をする際、広告ブロックをしていないにも拘わらず広告が出ず「ブロック解除して」という旨のメッセージが出て先に進めません。ブラウザ(Chrome) 、PC再起動で回避できることもあるのですが・・・先週ぐらいから発生してるような気がします。

[966]hassan (2022-10-20 09:02:09)
>管理人さんへ
>隠すようにした
のが、悪かったのか、あれ以来「難問ベスト50」のレベル0~6が出なくなりました。なぜかレベル7だけが出ています。

[953]管理人 (2022-10-11 12:50:35)
> hassanさん
隠すようにしました。ありがとうございます。

[952]hassan (2022-10-11 12:22:15)
>管理人さん
返信ありがとうございます。
なるほど、そういうことでしたか。
前後の問題は何事もなく開いたので、個人的には困ったことはありません。

[951]管理人 (2022-10-11 11:32:57)
> hassanさん
ご連絡ありがとうございます。
2021年は毎日ナンプレのレベル7は無いのでこんなことになるのですが
なんでそれが難問ベストにはいっちゃったんだろう???

[950]hassan (2022-10-11 10:53:35)
たまには難問やってみるかと思って開けたら、バグっぽい画面が出ました。
難問ベスト50 Lv.7 34番目 2021/7/19

[926]TINY24 (2022-09-18 09:51:56)
> 管理人さま
お返事ありがとうございます。
理解しました。今後、毎日のナンプレは、使う Chrome を統一します。2重データは管理人さんも気になるところかと思ったので、報告の意味も含めて質問しました。
過去問については、仕様上2重データになってしまいますが、気になるようでしたら処理して下さい。

[924]管理人 (2022-09-18 08:25:46)
> TINY24さま
ご無沙汰しております。
9月16日・レベル8ですがログインIDが別になっていました。
(ログインIDが違うのでTHE FIRST TAKEではどちらも別人の認識になるのでタイム登録できました。)
タイムが早い方を残しておきました。またなにかあればご連絡ください。

[923]TINY24 (2022-09-17 15:14:37)
お久しぶりです。いつもお世話になっています。
私事ですが、Chrome を古いバージョンで使用することになり、半月前のバージョンをポータブル版で使うことにしました。この影響で、データが2重登録になると思って、リセットして新たに始めることにしました。手順がまずかったのか、それとも不具合なのか(仕様なのか)、2重登録になってしまったようです。
THE FIRST TAKE 9月16日・レベル8をご確認下さい。

[916]みんみん (2022-09-13 05:17:51)
>管理人様
早速のご対応ありがとうございます。 滅多にないことですが気になっていたことでした。

[915]管理人 (2022-09-12 19:11:36)
> みんみんさま
こちらはなおったと思います。
どこから来たかをセッションというところに記録しているのですが
これが30分ぐらいで消えてしまうみたいで。
消えていても来たところはわかるのでそこに戻すようにしました。

[914]管理人 (2022-09-12 13:04:35)
> みんみんさま
ご連絡ありがとうございます。試してみます。
最近はナンプレ25の問題を作ろうかと思っているのですが
やっぱり25ともなると膨大でなかなかです。

[913]みんみん (2022-09-11 10:28:09)
以前から時々ある軽いバグですが、ナンプレを解いた後、「TOPに戻る」をクリックした際に戻れず、その時に表示されていた写真が変わるだけで何度クリックしても戻れません。 タイムを登録するか、ブックマークからログインし直せば良いだけなのですが、好記録を登録しないのに悪記録だけ登録するのも「なんだかなぁ」て気がして…
状況としては、正解するまでに30分あるいはそれ以上に時間を要した場合に多いです。
ブラウザはChromeですが、常時ウィンドウで3~4つ、タブで10個前後(多ければ20個ぐらい)開いてる状態です。

[904]ぷれ (2022-08-29 17:48:48)
>[901]管理人さま
ボタン修正、早速のご対応、ありがとうございます。
タイムの方は、旧画面で解答すると登録 表示されるのに
新画面で解答すると表示されないので不思議に思ったのです。
(ご提案のとおり、年齢性別を登録してみましたが
やはり新画面の方では表示されませんでした。)

[903]管理人 (2022-08-29 14:34:26)
> みんみんさん
ご提案ありがとうございます。
THE FIRST TAKEに関しては1回するとサーバに記録されるのですが
端末を変えるともしかしてクッキーの関係で出来てしまうのかもしれません。最初の一問をやめると人数が減りすぎるのではと恐れているのですがどうなんでしょう。ちょっと考えますね。
タイムの同期もありがとうございます。おかしいなぁ・・・汗
確認いたします。

[902]みんみん (2022-08-29 13:15:21)
THE FIRST TAKE について二点あります。
1) 動画広告に関して、
一問目をAという端末で解く際 広告は出ません。 その後間をおいてBという端末で二問目を解こうとするとやはり広告は出ません。 更にBという端末で続けて三問目を解こうとしたところで広告用ウィンドーがポップアップします。 Cという三台目端末を持ち合わせていないので確認できませんが、Cという端末で三問目をチャレンジした場合にはこうこくがでないのではないかと推測されます。
「最初の一問だけ広告なしで…」という条件はなくし、日付でフラグリセットし、「一度広告を見れば同日中は…」という仕様ではいかがでしょう? 気合い入れて「さぁ解こう」って時に広告で中断されるのは「なんだかなぁ、、、」って感じになってしまいます。
ちょっと愚痴っぽくなってしまい申し訳ありません。
2) 二台の端末でタイムの共有が一方通行になっているようです。
先日お教えいただいた方法でA→Bへのタイムは共有できていましたが、端末Bで解いた結果が端末Aに反映されていないようです。 念のため、端末Aでも一旦ログオフし、TOP画面からマイページにログインし直してもやはり出ませんでした。 今朝も端末Aで一問解いたあと、先程端末Bでアクセスしたところ、端末Aで解いたタイムが表示されていました。
この時に、1) の状況に遭遇し指摘させていただいた次第です。
以上、長文になり申し訳あありませんが、ご報告まで。 m(_ _)m

[901]管理人 (2022-08-29 10:43:12)
> ぷれさん
「↩やり直し」ボタン修正いたしました。
タイム登録の件ですが試したところ私の方は表示されています。
ぷれさんは年齢、性別が未設定で登録されていますので
年齢: 性別: 1st:を「全て」にしていただくとどうでしょうか?
また新画面もだいぶ候補の見落としとかが少なくなるのでお使いいただければ幸いです。

[900]管理人 (2022-08-28 08:31:28)
> ぷれさん
ご連絡ありがとうございます。
確認いたします。しばらくお待ちください。

[899]ぷれ (2022-08-27 10:53:13)
管理人さま、長年大変お世話になっております。
ナンプレ16の旧画面の 「↩やり直し」ボタンを押すと
1つではなく何個か前に一気に戻ってしまうのですが
確認していただけますでしょうか。
私は慣れの問題でまだしばらくはこちらを使う予定です。
新画面もトライしてみましたが、タイムが登録しても
表示されませんね。早くはないので関係ないんですけどね。

[894]管理人 (2022-08-22 18:28:27)
> みんみんさん
大丈夫です。お気になさらないでください。
今はいっそのこととナンプレ16をナンプレ京シンプル版のように
違う作り方にしようかと思っています。これだと2桁数字も変形をかけて収めることができるので。
またおかしいことがあればぜひご連絡ください。

[893]みんみん (2022-08-22 18:18:51)
>[892] 管理人さん
タイム云々は通常のナンプレの「次の一手」と混同してしまい問題ありませんでした、申し訳ありません。
問題提議の意図としては、途中で正誤を確認しようとして「ヒント」をクリックしてもメッセージが出ず、特に表示が変わることもなく、3回目までのカウンタが有効で4回目以降は警告だけ出る、ということを伝えたかった次第です。

[892]管理人 (2022-08-22 11:36:23)
> みんみんさん
ご報告ありがとうございます。
調べたのですがナンプレ16ではヒントを使ってもタイム加算はされませんね。4回目以降は「ヒントと無しでがんばってください」と出ます。
明らかに間違っているのに赤く表示されなかったところが問題なのですがプログラム見る限りは大丈夫そうなんですが、私の方はうまく動いたのでまた出てきたらキャプチャをアップしていただければと思います。
メモ数字はむずかしいですねぇ。2桁数字をうまく並べられなくて現在のような形になっています。ちょっと考えてみますね。

[887]みんみん (2022-08-19 17:46:57)
ナンプレ16で「ヒント」を使った場合に「3回まで・・・」のメッセージの後、正誤のコメントもなくタイムだけが加算され、更に4回目以降は「ヒント無しで・・・」と出ます。
明らかに何処かでミスっているはずの状態で「ヒント」を使って発生しましたので、間違ったセルにマーキングされることを期待しての操作で発生しました。
またバグではないのですが、メモ数字の配置が9マスのナンプレと異なり16分割(4x4)の配置ではないようなのでメモ数字が活用しにくいです。 例えば、下から2段め、右端であれば「12」かと思えば必ずしもそうではないので寧ろメモ数字を置かないほうが見やすい状況です。 まぁ、Lv1だからなのでしょうけど。

[883]みんみん (2022-08-17 10:56:11)
>[875] [877]
以前私が「832」で指摘した内容と同じ症状ではないかと思われます。
その後も「THE FIRST TAKE」を先に解いた際に意識して確認したところ、そのような症状が現れる日と、現れない日があるようです。

[877]管理人 (2022-08-14 11:10:55)
????????oyo????????さま
ご迷惑おかけして申し訳ないです。プログラムでおかしなところがないかまた点検いたします。
記録のリセットはこちらになります。
https://nanpre.adg5.com/mypage04.php
また下記では日付ごとにサーバに残っている記録が表示されるので
その日付に戻ることも可能です。まずはこちらをお試しいただければと思います。
https://nanpre.adg5.com/mypage02.php

[876]管理人 (2022-08-14 11:06:07)
> みんみんさん
フェス用のバックになってしまっていましたね。
失礼しました。修正しました。

[875]????????oyo???????? (2022-08-14 08:04:34)
管理人様 いつもお世話になっております。
じつは、昨日の毎日ナンプレLe8を回答した覚えがないのですが、回答時間が表示されていました。さらに、ベストテン(70歳)のタイムなのに欄に表示なっておりません。
気持ち悪いので google、yahoo の現在のログイン情報を白紙にして、新たなIDで登録できませんでしょうか。(間違って別スレに書いてしまいました。)


[873]みんみん (2022-08-14 06:45:21)
>管理人さん
ナンプレ画面のダークモードでの背景色が白色固定されているようで、非常に見づらいです。 ご対応よろしくお願いいたします。

[864]みんみん (2022-08-10 19:01:13)
>[857]、[863]
Lv.6は平均タイムより早い4分を切りましたが、むしろLv.8のほうが自力で解けず「次の一手」を数回利用したため惨憺たる結果になりました。

[863]管理人 (2022-08-10 18:50:21)
> ????????oyo????????さま
早く解かれたのかもしれないので(今日のLv6は難しかったですが・・・)ひきつづきおかしいようならご連絡ください。

[857]????????oyo???????? (2022-08-10 09:07:52)
本日の毎日ナンプレL6のタイムがおかしい。私の能力ではこんなタイムは出せない。確か、13分台だったような・・・・・┐(´~`;)┌

[850]管理人 (2022-08-05 10:13:21)
> 龍さん
ご報告ありがとうございます。
タイム周りは不正登録が横行していろいろ対策をしたのですが
なんかややこしいことになってしまったのかもしれません。。。。

[848]龍 (2022-08-04 07:03:46)
Androidスマホです。
あまりに酷いスコアで再チャレンジ後で2度目のスコアを登録する時、表示されるタイムが1度目のタイム。敢えてそのまま登録するをクリックすると2度目のタイムが1stとして登録されます。
証拠スクショはあるのですが…あまりに恥ずかしいタイムなので公開しかねますが……(笑)

[821]管理人 (2022-07-25 15:09:52)
> みんみんさま
すいません。以前報告があったバグの仲間だと思います。
当時、修正したつもりでしたがまたでてきてしまいました。
プログラムを見直して読み込む寸前にチェックするようにしました。
知らないタイムのデータを戻すには「マイページ」の下の方に
「バックアップデータの復元」があるのでご利用ください。
https://nanpre.adg5.com/mypage02.php

[820]みんみん (2022-07-25 05:56:30)
「毎日ナンプレ」プレイ中にうっかりウィンドーを閉じてしまい、再度ログインして再調整しようとしたところ、未挑戦レベルも全てタイムが登録されていました。

[744]するめ (2022-06-21 23:22:56)
>みんみんさん
ご推察の通り、チェックボックスがオフになっていました。オンにしたら解決しました。ありがとうございます!

[743]みんみん (2022-06-21 21:51:42)
>するめさん
私の場合、最近のMicsosoftのwindows updateのあと、個人用の設定(ダークモード)が初期化されていました。
するめさんの場合、「毎日ナンプレ」の「候補もコピー(テスト)」のチェックボックスが外されていませんか?

[742]するめ (2022-06-21 11:08:56)
気づいたのは昨日ですが、候補数字がハイライトしなくなっています。私だけでしょうか。環境は、PC、Chrome最新版です。

[734]みんみん (2022-06-18 08:51:15)
>管理人さん
たまに早く目が覚めて4時前後ということもありますが、大体5時前後からやり始めます。
今朝も4時過ぎくらいに目が覚めたので、頭を覚醒させrために「THE FIRST TAKE」をやり始め、その後「毎日ナンプレ」をやってて気づいた次第です。何か見覚えのあるタイムでしたので確認したら添付画像のようにドンピシャでした。

[733]管理人 (2022-06-18 07:40:06)
> みんみんさん
ご連絡ありがとうございます。確認いたします。
時間は0時回ってすぐとかそういうことはありませんか?



[732]みんみん (2022-06-18 06:35:32)
少し前から「あれっ?」と思っていたのですが、
・「毎日ナンプレ」でプレイする前からタイムが表示されるケースがあります。
・「THE FIRST TAKE」で初回にも拘らず「初回限定」の旨の通知が出て選択画面に戻されます。
「THE FIRST TAKE」についてはうっかりダブルクリックしてしまったことが原因かもしれませんが、画面が切り替わろうとする前の動作なのでやはり挙動としてはおかしいのではないかと思います。
また「毎日ナンプレ」の方は、「THE FIRST TAKE」とクロスリンクしているようで、「THE FIRST TAKE」を先にプレイした場合、そのタイムが「毎日ナンプレ」に表示されるようです。

