Solving Techniques 3
Hidden Pairs/Triples/Quads

Like the naked pairs, this method involves looking for pairs like [1,2][1,2], in cases where these pairs are hidden. Since they are hidden numbers, they are harder to find, but when you find them, [1,2] can be eliminated as candidates from other cells.

Hidden Triples

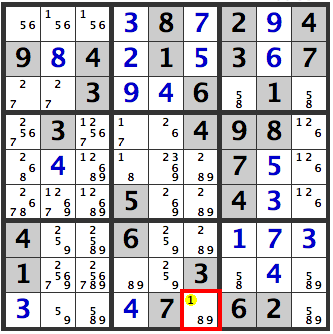
Lets have a look at the center-right box. 4,5,6 in column 9 are [1,2,5,6][1,2,5,6][1,2,6].
In [R3C9]’s [5,8,9], a 1, 2, or 6 can’t be entered.
Also, in [R8C9]’s [5,8,9], a 1, 2, or 6 can’t be entered.
It appears that a 1 might fit in [R9C9], but since 1 can only go in row [7] in column [7], it is impossible.
Hence, a triple of [1,2,6] arises in 4,5,6 of column 9.

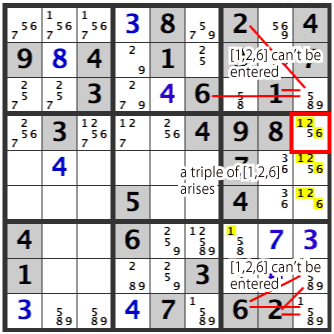
Therefore, [1,2,6] can’t be entered in the other cells of this box. Hence, a [5] in [R5C8] and a [3] in [R6C8] are confirmed.

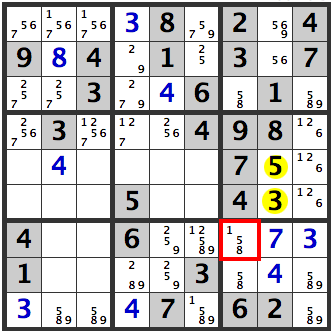
[1] in [R7C7] is also confirmed.

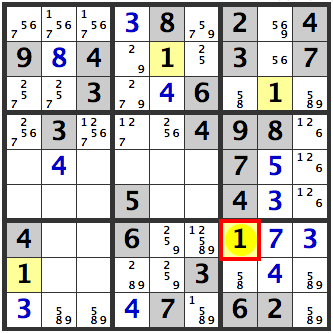
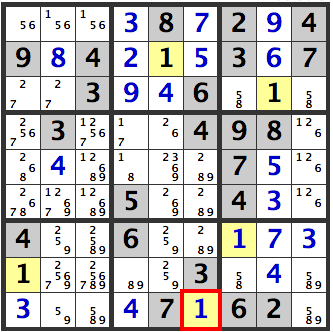
Hidden Triples-2

It’s not quite hidden, but a triple of 1,7,8 arises between [R4C4], [R5C4] and [R8C4]. The 1 will have to be in either [R4C4] or [R5C4], so it will not be in [R5C6] or [R6C6].

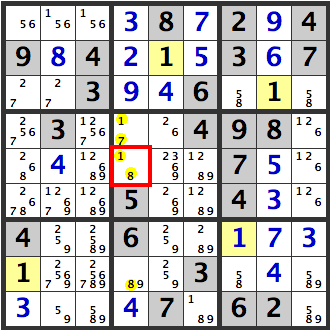
Hence, 1 in [R9C6] is confirmed.

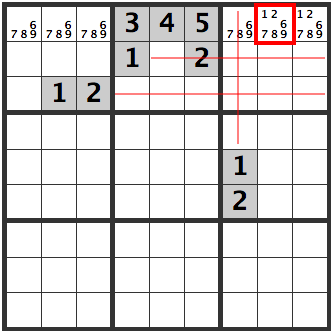
Hidden Pairs

As seen in the diagram below, if 1,2 is in the upper left and upper middle, and there is also 1,2 in column 7, [R1C8] and [R1C9] in the upper right box will become [1,2][1,2]

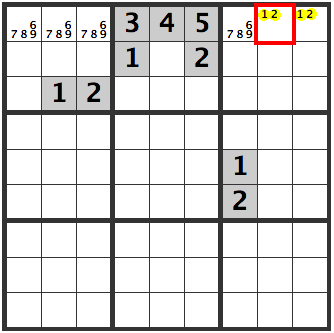
Since a [1,2] pair is now in the upper right box, 1 and 2 can’t be entered in the other cells.

Hidden Quads

Quads are made up of four numbers in the same way, but we couldn’t find a specific example for this. It will appear as if there are many candidates, but if a number can’t be entered in any of the other cells, this technique will work.
It is a bit difficult, but it is an effective technique when you get stuck.

Names of cells in Sudoku

R1C1	R1C2	R1C3	R1C4	R1C5	R1C6	R1C7	R1C8	R1C9
R2C1	R2C2	R2C3	R2C4	R2C5	R2C6	R2C7	R2C8	R2C9
R3C1	R3C2	R3C3	R3C4	R3C5	R3C6	R3C7	R3C8	R3C9
R4C1	R4C2	R4C3	R4C4	R4C5	R4C6	R4C7	R4C8	R4C9
R5C1	R5C2	R5C3	R5C4	R5C5	R5C6	R5C7	R5C8	R5C9
R6C1	R6C2	R6C3	R6C4	R6C5	R6C6	R6C7	R6C8	R6C9
R7C1	R7C2	R7C3	R7C4	R7C5	R7C6	R7C7	R7C8	R7C9
R8C1	R8C2	R8C3	R8C4	R8C5	R8C6	R8C7	R8C8	R8C9
R9C1	R9C2	R9C3	R9C4	R9C5	R9C6	R9C7	R9C8	R9C9