Sponsored Links

TOP > Techniques > Hidden Unique Rect's.

Solving Techniques 17
Hidden Unique Rect's.

This is a method of finding hidden unique rectangles.
Below, the [6] in the [156] is X’d out. It can be eliminated as a candidate.

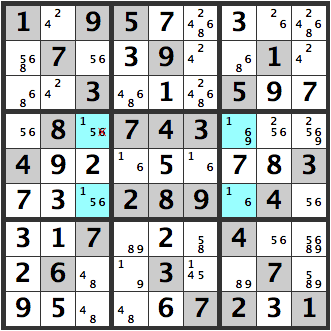
If the upper left blue [156] cell is a [1], then [6] can’t be a candidate for this cell.

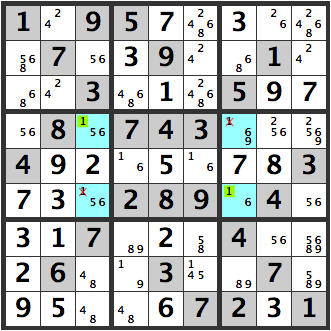
A problem arises when the blue [156] is any number other than [1]. The yellow parts become candidates for [1].

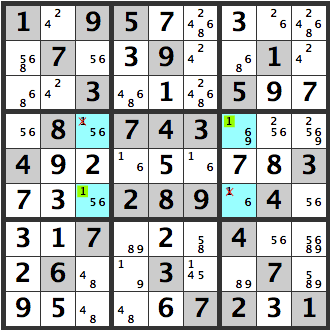
Then the lower right blue cell would be a [6], since it is a [16]. In this case, too, if the upper left, blue cell is a [6]…

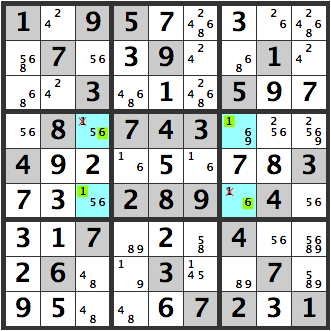
we eventually arrive at the following diagram.

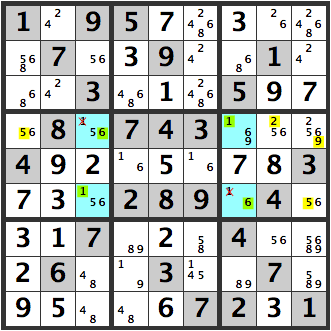
But lets step back. The four blue cells create a unique rectangle with [16][16], leading to multiple solutions. Therefore, in this case, the blue cell to the upper left is a [5] and not a [6].

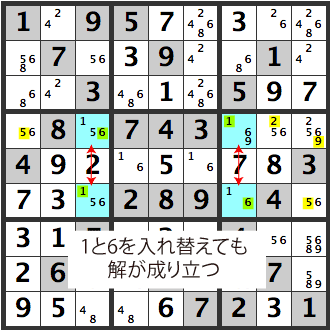
Hence, this [6] can be removed as a candidate. Otherwise, we are left with a Sudoku problem which doesn’t work.

Hidden Unique Rect's. 2

Below is also a hidden unique rectangle. The X’d out [6] can be removed as a candidate from [R4C3]. (The 8s in the same row form a strong link)

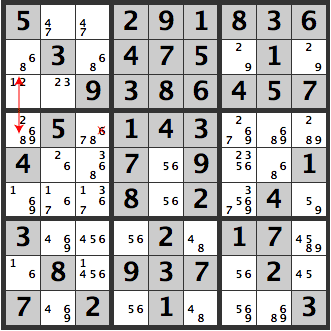
If the [68] in the upper left [R2C1] is an [8], then [R2C3] becomes a [6], so the X’d out [6] in [R4C3] can’t be entered there.

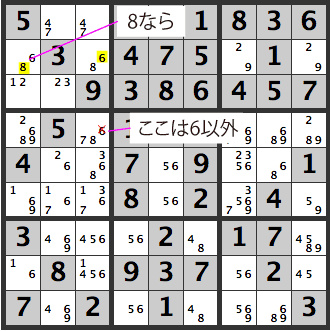
If the upper left [R2C1]’s [68] is a [6], we have a problem. In this case, there are only two [8]’s in the same row, so even if there are many candidates for [R4C1], it will be an [8]. Furthermore, [R2C3] will also be an [8]. If [R4C3] is a [6], we have a unique triangle where [6] and [8] are interchangeable.

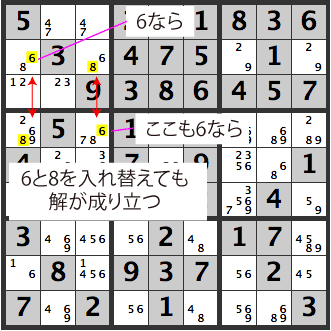
It will hence, not work as a Sudoku problem, and [6] can be removed as a candidate.

reference: sudokuwiki.org

Names of cells in Sudoku

R1C1	R1C2	R1C3	R1C4	R1C5	R1C6	R1C7	R1C8	R1C9
R2C1	R2C2	R2C3	R2C4	R2C5	R2C6	R2C7	R2C8	R2C9
R3C1	R3C2	R3C3	R3C4	R3C5	R3C6	R3C7	R3C8	R3C9
R4C1	R4C2	R4C3	R4C4	R4C5	R4C6	R4C7	R4C8	R4C9
R5C1	R5C2	R5C3	R5C4	R5C5	R5C6	R5C7	R5C8	R5C9
R6C1	R6C2	R6C3	R6C4	R6C5	R6C6	R6C7	R6C8	R6C9
R7C1	R7C2	R7C3	R7C4	R7C5	R7C6	R7C7	R7C8	R7C9
R8C1	R8C2	R8C3	R8C4	R8C5	R8C6	R8C7	R8C8	R8C9
R9C1	R9C2	R9C3	R9C4	R9C5	R9C6	R9C7	R9C8	R9C9

• TOP
• My page(Login)
• Daily Sudoku
• Back Numbers
• Sudoku puzzles
• LEVEL:1 ->LEVEL:2
• LEVEL:3 ->LEVEL:4
• LEVEL:5 ->LEVEL:6
• LEVEL:7 ->LEVEL:8
• Sai(彩) mode Sudoku puzzles
• LEVEL:1 ->LEVEL:2
• LEVEL:3 ->LEVEL:4
• LEVEL:5 ->LEVEL:6
• LEVEL:7
• Sudoku 16
• LEVEL:1 ->LEVEL:2
• LEVEL:3 ->LEVEL:4
• LEVEL:5 ->LEVEL:6
• LEVEL:7
• Sudoku 6
• LEVEL:1 ->LEVEL:2
• LEVEL:3 ->LEVEL:4
• LEVEL:5
• Average time
• Top 300 difficult puzzles
• High Score
• Medals
• Rules
• Sudoku Tricks
• Solving Techniques
• Hidden Singles
• Naked Pairs/Triples/Quads
• Hidden Pairs/Triples/Quads
• Pointing Pairs
• X-Wing
• Y-Wing
• Simple Coloring
• Simple Chain
• Sword-Fish
• XYZ-Wing
• X-Cycles
• BUG+1
• XY-Chains
• Jelly Fish
• Unique Rectangles
• Extended Unique Rect.
• Hidden Unique Rect's
• WXYZ-Wing
• Aligned Pair Exclusion
• Sudoku problem solver program
• How to create Sudoku problems
• 1 Creating the answer
• 2 Creating blank boxes
• 3 Sudoku solver program
• 4 Creating problems with fewer clues
• About Sudoku (column)
• About Sudoku
• Possible combinations of Sudoku
• About Sudoku techniques
• Contact
• Download