

Sponsored Links
TOP > Techniques > XYZ-Wing
Solving Techniques 10
XYZ-Wing
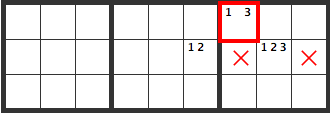
The XYZ-Wing is different from XY, in that three numbers are used. It is like the diagram below. When a problem turns out like this, a 3 will be entered somewhere.

If a 3 is entered in [R1C2], then it can’t be in the cells marked X, as shown below.

If a 3 is entered in [R1C5], then it can’t be in the cells marked X, as shown below.

If a 3 is entered in [R2C3], then it can’t be in the cells marked X, as shown below.

As you can see below, in the overlapping areas, X, a 3 can’t be entered.

Sponsored Links
Below is another XYZ wing, but not using [123] candidates, but rather a combination of three types of candidates, [12][23] and [13].

If a 3 is entered in [R2C3], it can’t be entered in the cells marked X, as shown below.

If a 3 is entered in [R1C5], it can’t be entered in the cells marked X, as shown below.

Hence, in the overlapping areas marked X, a 3 can’t be entered, as shown below. There are more X’s than in the previous example.

The numbers can also be further apart, as shown below. As in the previous examples, 3’s can’t be entered where the X’s are.

They can also be close together, as shown below. In this case, the common number is [1], so 1 can’t be entered in the cells with X’s.
This technique is an application of the XY-wing technique, so it seems to be easy to learn.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links

