Solving Techniques 11
X-Cycles

Before considering X-Cycles, it’s important to understand strong links and weak links.

Strong link

As shown below, a link where only two numbers are possible in a row, column or box, is called a strong link. In the diagram, it is between [1] and [2].

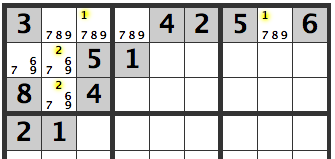
Weak link

As shown below, a weak link is a link where there are more than three numbers that are possible within a row, column or box. [1] and [2] are in three possible cells, which creates a weak link.

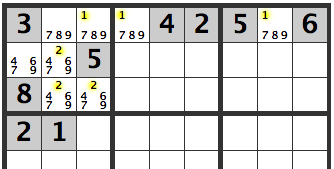
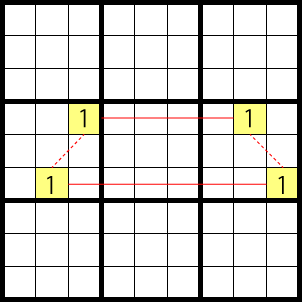
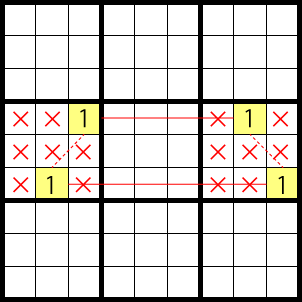
X-Cycles

The most simple X-cycle is shown in the diagram below. The red line is the strong link, the dotted red line, the weak link.

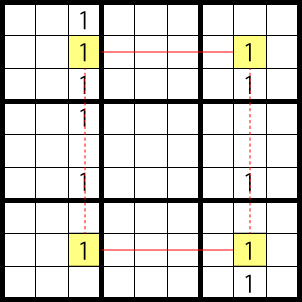
This works the same way as an X-wing and it always works out to:
1　
　1
or
　1
1　
Hence, 1 can’t be entered in the areas marked X.

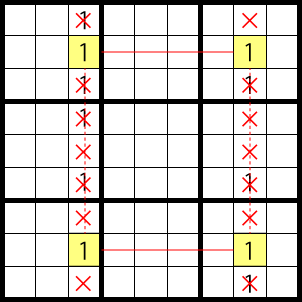
So the X-cycle, of a given number, refers to a
cell - strong - cell - weak - cell - strong - cell
or
cell - strong - cell - weak - cell - strong - cell - weak - cell - strong - cell
type of loop that begins and ends with a strong link. (It also works, if there are strong links, instead of weak within the pattern.)
The number in the weak links can be removed as candidates, but these cells change depending on the situation.

X-Cycles 2

This is a slightly complex pattern. The red line is a strong link, the dotted red line is a weak link.

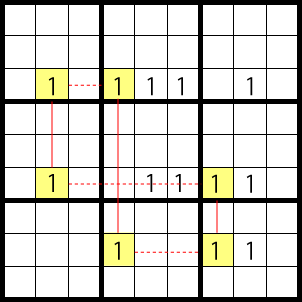
Where the 1 goes is in one of the two patterns below.

Pattern A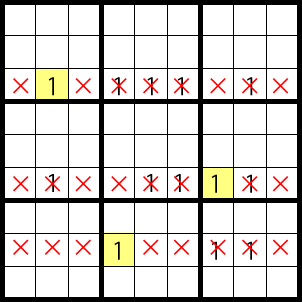

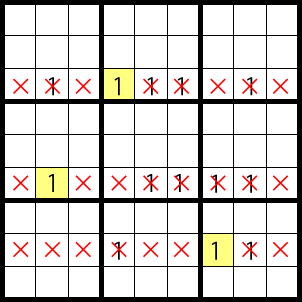
Pattern B

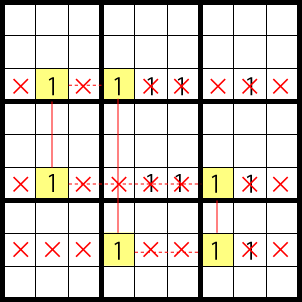
Hence, in the overlapping areas X, 1 can’t be entered, as shown below.

X-Cycles 3

Below is another complex pattern. The red line is a strong link, the dotted red line is a weak link.

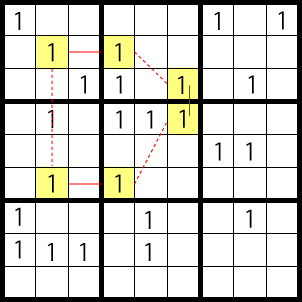
Where the 1 goes, is in one of two patterns below.

Pattern A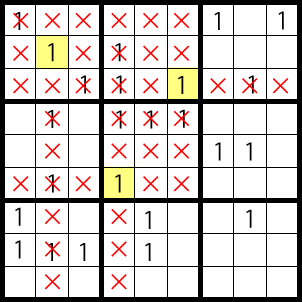

Pattern B

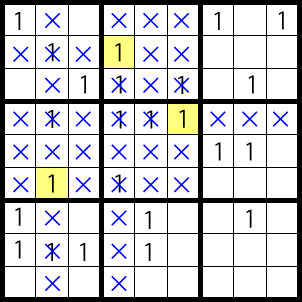
When the two patterns are combined, it becomes like the diagram below.

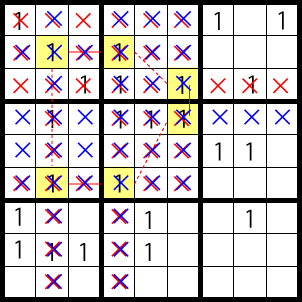
And in the overlapping areas marked X, a 1 can’t be entered. (The X’s of the strong link are not shown.)

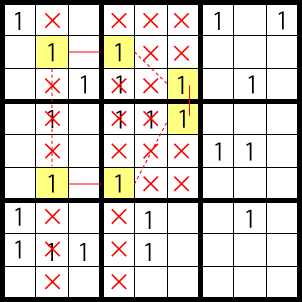
X-Cycles 4

Below is an easy pattern.

As you can see, 1 can’t be in the areas marked with X’s.
Examining the samples, in each case, the connection in the weak link, if it is a row or column, that row/column’s other cells are removed as candidates. If it is a box, the box’s other cells are removed as candidates.

If you can use this technique, you are quite accomplished at Sudoku.

Names of cells in Sudoku

R1C1	R1C2	R1C3	R1C4	R1C5	R1C6	R1C7	R1C8	R1C9
R2C1	R2C2	R2C3	R2C4	R2C5	R2C6	R2C7	R2C8	R2C9
R3C1	R3C2	R3C3	R3C4	R3C5	R3C6	R3C7	R3C8	R3C9
R4C1	R4C2	R4C3	R4C4	R4C5	R4C6	R4C7	R4C8	R4C9
R5C1	R5C2	R5C3	R5C4	R5C5	R5C6	R5C7	R5C8	R5C9
R6C1	R6C2	R6C3	R6C4	R6C5	R6C6	R6C7	R6C8	R6C9
R7C1	R7C2	R7C3	R7C4	R7C5	R7C6	R7C7	R7C8	R7C9
R8C1	R8C2	R8C3	R8C4	R8C5	R8C6	R8C7	R8C8	R8C9
R9C1	R9C2	R9C3	R9C4	R9C5	R9C6	R9C7	R9C8	R9C9

TOP
BACK NUMBERS
HIGH SCORE
Sudoku puzzles lv.1 | lv.2 | lv.3 | lv.4 | lv.5 | lv.6 | lv.7 | lv.8
Rules
Download

Solving Techniques 11 X-Cycles