

Sponsored Links
TOP > Techniques > Sword-Fish
Solving Techniques 9
Sword-Fish
This is a situation where the 1 is only possible in three places, like columns 2, 5 and 8, below. (there are only three cells where 1 can be, in the columns indicated with red lines, and they occur in the same rows)
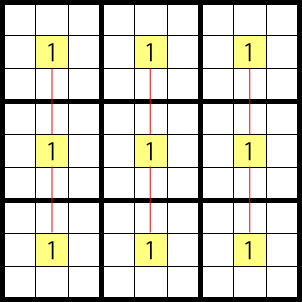
In this case, the 1’s can’t be in the places marked with x’s as pictured below, so they can be eliminated as candidates.
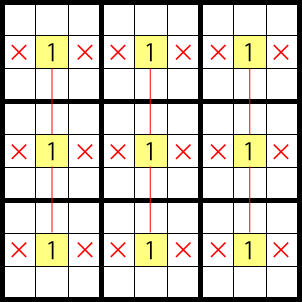
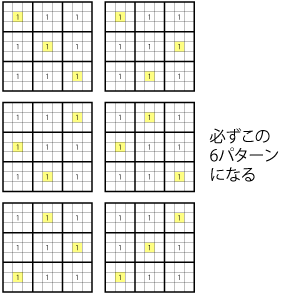
When examined, you see that there are only six ways in which the 1 can be entered, and that indeed, they can’t be entered where the x’s are.
As a variation there is a pattern like the one below.
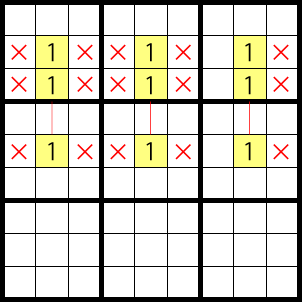
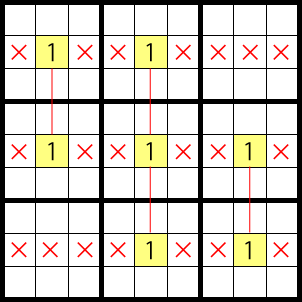
It’s a very efficient technique when this pattern actually happens, since you can eliminate lots of candidates at once.
Sponsored Links
Finned Sword-Fish
As in the diagram below, when there are many candidates for 1 in the middle column only, it is called a finned sword fish. The cells indicated with x only, can be eliminated as candidates for 1. (also possible when the pattern is not in the center)
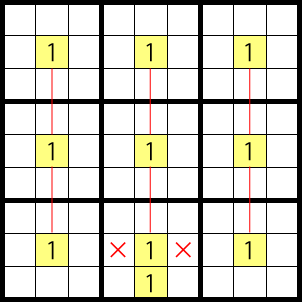
Lets examine if this is true. As shown below, if there is a 1 in the ‘fin’ area, there can’t be another 1, other than in this box. However, in column 2 and column 8, there are three places each for where 1 could be. Therefore, the possibilities can’t be eliminated the same way as they can, when there are no fins.
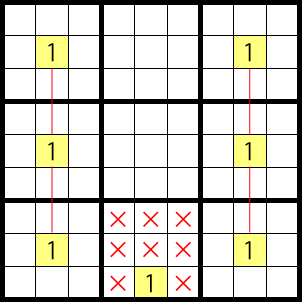
As shown below, if a part that is not the fin becomes a 1, then a 1 can’t be in 3 rows, just as it would, when there are no fins.
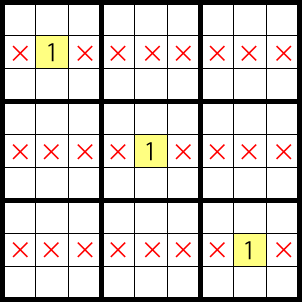
Therefore, the candidates that can be eliminated based on the overlap, are the cells that would get eliminated in a swordfish, but only within the box, which the fin is located in.

The swordfish is quite challenging, but when examined, it does hold up to be true.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links

