

Sponsored Links
TOP > Techniques > WXYZ Wing
Solving Techniques 18
WXYZ Wing
In a pattern like the one below, the red Z can be removed as a candidate.
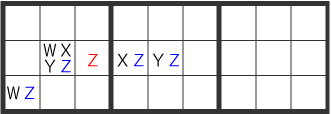
For an example, please look below. The [9] comes up in all cells. This [9] is the [Z].
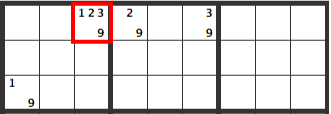
If the lower left [19] cell is a [9], obviously a [9] can’t be entered in the other cells of this box.
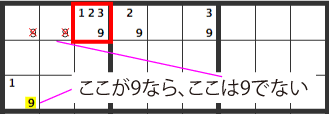
If the lower left [19] cell is a [1], then a [9] has to be entered somewhere in the upper line, and it can’t be in the place indicated on the diagram.
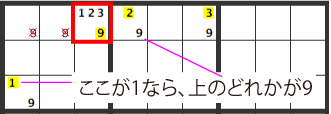
The WXYZ Wing is a technique which uses a combination of four cells and four candidate numbers to eliminate candidates from other cells.
WXYZ Wing 2
This pattern is also a WXYZ wing. “Which number?” You might ask. It is the [5]. Lets examine together.
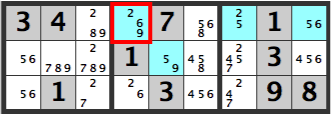
If, in the diagram below, the [59] in the center box is a [5], the [5]’s from the same box and same line will be eliminated as candidates.
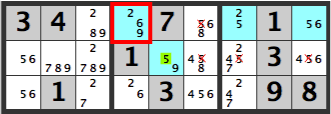
If, in the diagram below, the [59] in the center box is a [9], either one of the right hand box’s blue cells will become a 5.
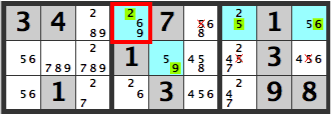
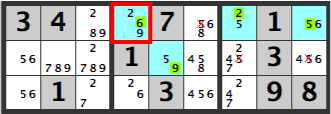
Therefore, the X’s, which apply in both cases, can be eliminated as candidates.
Sponsored Links
WXYZ Wing 3
This pattern is also an WXYZ wing. It is quite a distorted pattern. The [4] will be [Z]. Lets examine together.

If, in the diagram below, the left box’s [14] cell is a [4], then the [4]’s in the same row can be eliminated as candidates.

If, in the diagram below, the left box’s [14] cell is a [1], the blue cell in the right box will be a [4].

しTherefore, the X’s, which apply in both cases, can be eliminated as candidates.
WXYZ Wing 4
Here we have a distorted pattern again. There are a variety of patterns, so it’s good to look for four cells and four numbers.
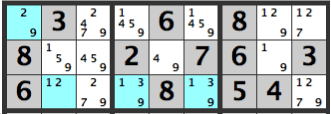
If, in the diagram below, the left box’s [29] cell is a [9], then the [9]’s in the same row can be eliminated as candidates.
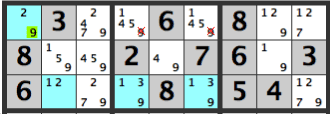
If, in the diagram below, the left box’s [29] cell is a [2], then the [9] would be one of the two cells in the center box.
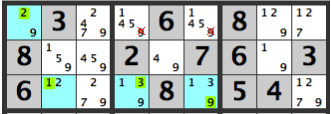
Therefore, the X’s, which apply in both cases, can be eliminated as candidates.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links


