

Sponsored Links
TOP > Techniques > Unique Rectangles
Solving Techniques 15
Unique Rectangles
The cells that that contain [12] in the diagram below would work as both:
1 2
2 1
or
2 1
1 2
It can be either solution.
We presume that a Sudoku problem can’t have two solutions.
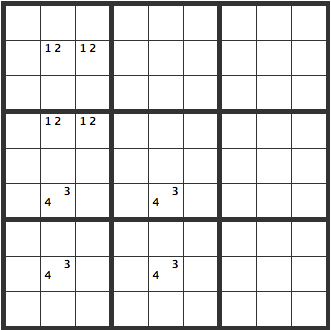
[34], on the other hand, can’t be switched around. They wouldn’t be switched within the same box, so the numbers can’t be switched.
Unique Rectangles 1
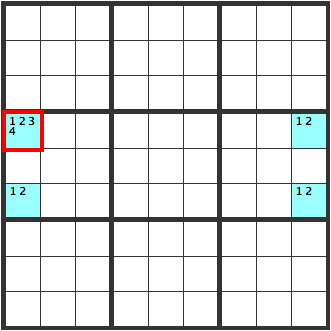
Like the diagram, this is a pattern where the [12] can be switched around. If it can be switched, it wouldn’t work as a Sudoku problem, so in the cells indicated in red, either a [3] or [4] is entered.
Unique Rectangles 2
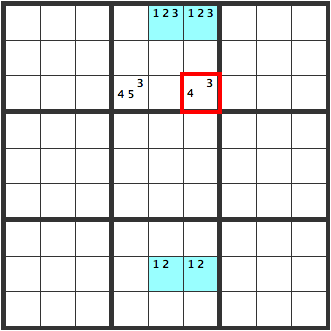
In this pattern, one of the upper two cells with [123], will definitely be a [3]. Hence, [3] won’t go in the cell marked red and it will be a [4].
Unique Rectangles 3
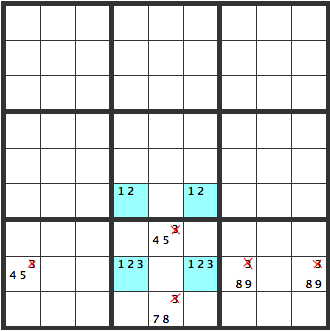
In this pattern, one of the lower two cells with [123], will definitely be a [3]. That means, [3] can’t be in the other cells in the box. Also, a [3] can’t be entered in line H of the boxes to the left and right.
Sponsored Links
Unique Rectangles 4
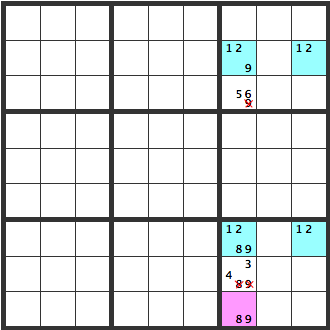
An [8] or [9] will definitely be entered in either the [129] cell or [1289] cell. There is a cell at the very bottom with [89] as candidates. If an [8] is entered in the blue cell above, then the pink cell will be a [9]. If the blue cell is a [9], then the pink cell will be an [8], so [8] or [9] can’t be entered in the cells marked with X’s.
Unique Rectangles 5
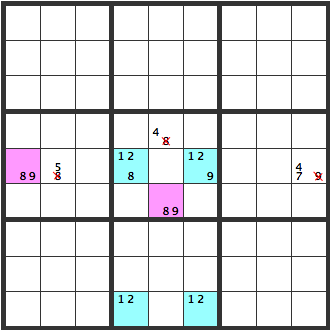
An [8] or [9] will definitely be entered in the [128] cell or [129] cell. The pink cell only has [89] as candidates. This means if an [8] or [9] is entered into either one of the blue cells, the pink cells will become [8] or [9], so [8][9] can’t be entered into the cells marked with X’s.
Unique Rectangles 6
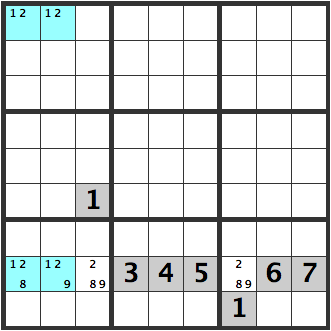
An [8] or [9] will go into either one of the [128][129] cells below. However, there are no open cells in this line where a [1] can be entered. Therefore, a [1] will have to go in one of the blue cells below, so a [2] can’t be entered into one of the blue cells at the bottom.
Unique Rectangles 7
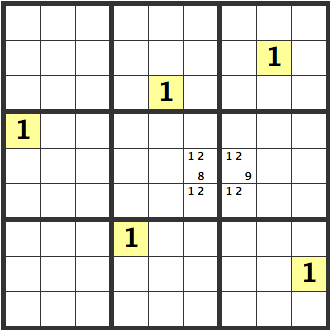
Lets examine the [128][129] cells. In this line, a [1] can’t be entered into any of the empty cells. This means, in either one of the [128][129] cells a [1] has to be entered, and [2] can be eliminated as a candidate.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links

