

Sponsored Links
TOP > Techniques > XY-Chains
Solving Techniques 13
XY-Chains
As shown below, there is a chain from the red cell’s [12] going to [23] [34] [14].
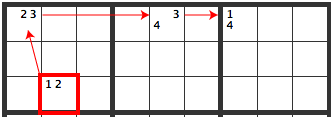
If [R3C2] is [1], the result is as follows.
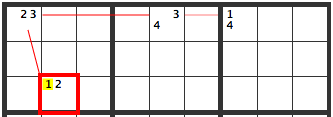
If [R3C2] is [2], the result is as follows.
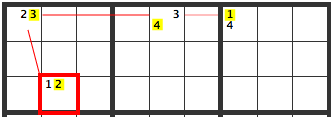
In either solution, 1 would not be in the overlapping area X.
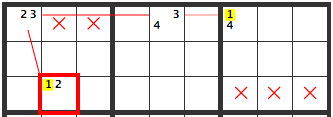
This situation is known as an XY-chain.
XY-Chains 2
This is another pattern. As seen below, [23], [34], [14] is linked to the red cell [12].
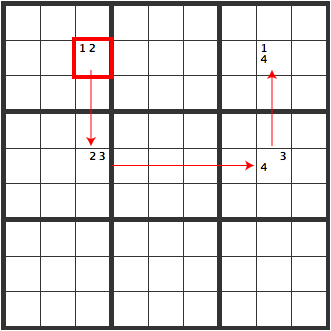
If [R2C3] is [1], the result is as follows.
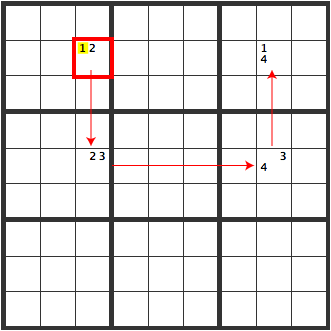
If [R2C3] is [2], the result is as follows.
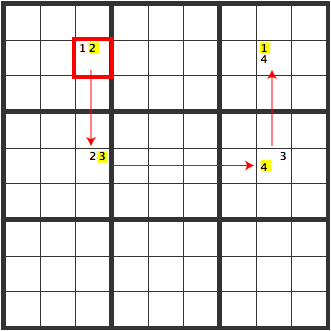
In either position of 1, 1 can’t be entered in the overlapping area X.
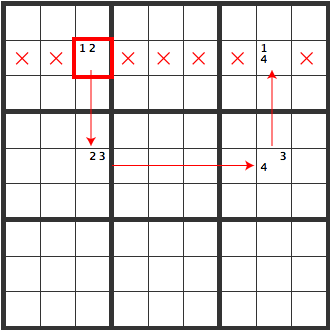
These are rarely seen in actual problems. However, when you are solving a very advanced problem and get stuck, it is a good technique to remember.
Sponsored Links
XY-Chains 3
We made a slightly different pattern. As shown below, the red [12] is linked to [23][34][34][45][15].
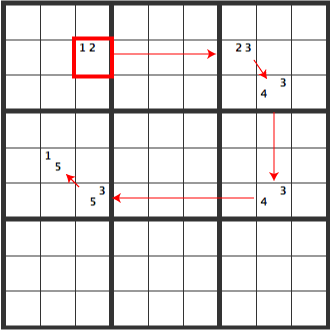
If [R2C3] is [1], the result is as follows.
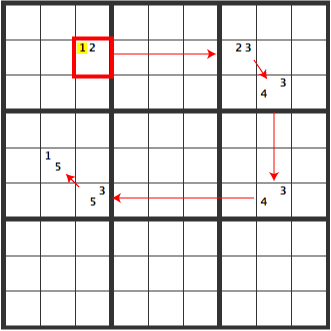
If [R2C3] is [2], the result is as follows.
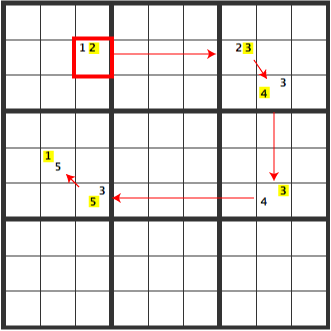
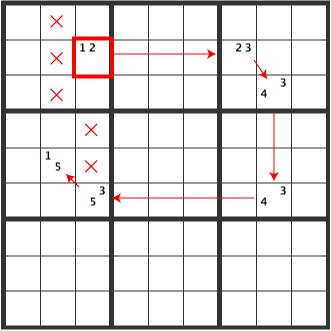
In either position of 1, there can’t be 1’s in the overlapping area X.
Names of cells in Sudoku
| R1C1 | R1C2 | R1C3 | R1C4 | R1C5 | R1C6 | R1C7 | R1C8 | R1C9 |
| R2C1 | R2C2 | R2C3 | R2C4 | R2C5 | R2C6 | R2C7 | R2C8 | R2C9 |
| R3C1 | R3C2 | R3C3 | R3C4 | R3C5 | R3C6 | R3C7 | R3C8 | R3C9 |
| R4C1 | R4C2 | R4C3 | R4C4 | R4C5 | R4C6 | R4C7 | R4C8 | R4C9 |
| R5C1 | R5C2 | R5C3 | R5C4 | R5C5 | R5C6 | R5C7 | R5C8 | R5C9 |
| R6C1 | R6C2 | R6C3 | R6C4 | R6C5 | R6C6 | R6C7 | R6C8 | R6C9 |
| R7C1 | R7C2 | R7C3 | R7C4 | R7C5 | R7C6 | R7C7 | R7C8 | R7C9 |
| R8C1 | R8C2 | R8C3 | R8C4 | R8C5 | R8C6 | R8C7 | R8C8 | R8C9 |
| R9C1 | R9C2 | R9C3 | R9C4 | R9C5 | R9C6 | R9C7 | R9C8 | R9C9 |
Sponsored Links

